Калькулятор Лейбница

Первая счетная машина, позволявшая производить умножение и деление также легко, как сложение и вычитание, была изобретена в Германии в 1673 году Готфридом Вильгельмом Лейбницем (1646-1716), и называлась «Калькулятор Лейбница».

Идея создать такую машину у Вильгельма Лейбница появилась после знакомства с голландским астрономом и математиком Христианом Гюйгенсом. Видя нескончаемые вычисления, которые астроному приходилось производить, обрабатывая свои наблюдения, Лейбниц решил создать устройство, которое ускорило и облегчило бы эту работу.

Первое описание своей машины Лейбниц сделал в 1670 году. Через два года ученый составил новое эскизное описание, на основе которого в 1673 году построил действующее арифметическое устройство и продемонстрировал его в феврале 1673 года на заседании Лондонского Королевского общества. В заключение своего выступления он признал, что устройство не совершенно, и пообещал его улучшить.

В 1674 – 1676 годах Лейбниц провел большую работу по улучшению изобретения и привез в Лондон новый вариант калькулятора. Это была малоразрядная модель счетной машины, не пригодная для практического применения. И только в 1694 году Лейбниц сконструировал 12 разрядную модель. Впоследствии калькулятор несколько раз дорабатывался. Последний вариант был создан в 1710 году. По образцу двенадцатиразрядной счетной машины Лейбница в 1708 году профессор Вагнер и мастер Левин создали шестнадцатиразрядную счетную машину.

Как видно, работа над изобретением была длительной, но не непрерывной. Лейбниц одновременно трудился в самых разных областях науки. В 1695 году он писал: «Уже свыше двадцати лет назад французы и англичане видели мою счетную машину. с тех пор Ольденбург, Гюйгенс и Арно, сами или через своих друзей, побуждали меня издать описание этого искусного устройства, а я все откладывал это, потому что я сперва имел только маленькую модель этой машины, которая годится для демонстрации механику, но не для пользования. Теперь же с помощью собранных мною рабочих готова машина, позволяющая перемножать до двенадцати разрядов. Уже год, как я этого достиг, но рабочие еще при мне, чтобы можно было изготовить другие подобные машины, так как их требуют из разных мест».

Работа над калькулятором Лейбницу обошлась в 24 000 талеров. Для сравнения, годовая зарплата министра по тем временам составляла 1 – 2 тысячи талеров.

К сожалению, с полной уверенностью не об одной из сохранившихся моделей калькулятора Лейбница нельзя сказать, что она была создана именно автором. Из-за чего существует много предположений относительно изобретения Лейбница. Есть мнения, что ученый только высказал идею применения ступенчатого валика, или что он не создавал калькулятор целиком, а только демонстрировал работу отдельных механизмов устройства. Но, несмотря на все сомнения, можно точно утверждать, что идеи Лейбница надолго определили путь развития вычислительной техники.

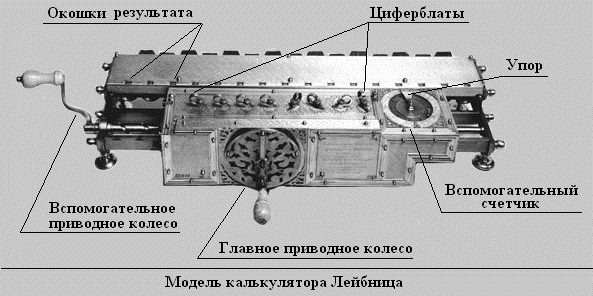
Мы будем вести описание калькулятора Лейбница на основе одной из сохранившихся моделей, находящейся в музее в Ганновере. Она представляет собой ящик около метра длинной, 30 сантиметров шириной и около 25 сантиметров высотой.

Изначально, Лейбниц пытался лишь улучшить уже существующее устройство Паскаля, но вскоре он понял, что операция умножения и деления требуют принципиально нового решения, которое бы позволяло вводить множимое только один раз.

О своей машине Лейбниц писал: «Мне посчастливилось построить такую арифметическую машину, которая бесконечно отличается от машины Паскаля, так как моя машина дает возможность совершать умножение и деление над огромными числами мгновенно, притом не прибегая к последовательному сложению и вычитанию».

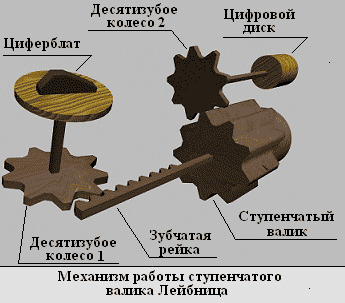
Это стало возможно, благодаря разработанному Лейбницем цилиндру, на боковой поверхности которого, параллельно образующей, располагались зубья различной длины. Этот цилиндр получил название «Ступенчатый валик».

К ступенчатому валику крепится зубчатая рейка. Эта рейка входит в сцепление с десятизубым колесом №1, к которому прикреплялся циферблат с цифрами от 0 до 10. Поворотом этого циферблата задается значение соответствующего разряда множимого.

Например, если второй разряд множимого равнялся 5, то циферблат, отвечающий за установку этого разряда, поворачивался в положение 5. В результате десятизубое колесо № 1, с помощью зубчатой рейки, так перемещало ступенчатый валик, что при повороте на 360 градусов он входит в зацеплении с десятизубым колесом № 2 только пятью наиболее длинными ребрами. Соответственно, десятизубое колесо №2 поворачивалось на пять частей полного оборота, на столько же поворачивался и связанный с ним цифровой диск, отображающий результирующее значение выполненной операции.

При следующем обороте валика на цифровой диск снова перенесется пятерка. Если цифровой диск совершал полный оборот, то результат переполнения переносился на следующий разряд.

Поворот ступенчатых валиков осуществлялся с помощью специальной ручки – главного приводного колеса.

Таким образом, при выполнении операции умножения не требовалось многократно вводить множимое, а достаточно вести его один раз и повернуть ручку главного приводного колеса столько раз, на сколько необходимо произвести умножение. Однако, если множитель будет велик, то операция умножения займет длительное время. Для решения этой проблемы Лейбниц использовал сдвиг множимого, т.е. отдельно происходило умножение на единицы, десятки, сотни и так далее множителя.

Для возможности сдвига множимого устройство было разделено на две части — подвижную и неподвижную. В неподвижной части размещался основной счетчик и ступенчатые валики устройства ввода множимого. Установочная часть устройства ввода множимого, вспомогательный счетчик и, главное, приводное колесо располагаются на подвижной части. Для сдвига восьмиразрядного множимого использовалось вспомогательное приводное колесо.

Так же для облегчения умножения и деления Лейбниц разработал вспомогательный счетчик, состоящий из трех частей.

Наружная часть вспомогательного счетчика — неподвижная. На ней нанесены числа от 0 до 9 для отсчета количества сложений множимого при произведении операции умножения. Между цифрами 0 и 9 расположен упор, предназначенный остановить вращение вспомогательного счетчика, когда штифт достигнет упора.

Средняя часть вспомогательного счетчика – подвижная, которая служит для отсчета количества сложений при умножении и вычитаний при делении. На ней имеется десять отверстий, напротив цифр внешней и внутренней частей счетчика, в которые вставляется штифт для ограничения вращения счетчика.

Внутренняя часть — неподвижная, которая служит для отчета количества вычитаний при выполнении операции деления. На ней нанесены цифры от 0 до 9 в обратном, относительно наружной части, порядке.

При полном повороте главного приводного колеса средняя часть вспомогательного счетчика поворачивается на одно деление. Если предварительно вставить штифт, например, в отверстие напротив цифры 4 внешней части вспомогательного счетчика, то после четырех оборотов главного приводного колеса этот штифт наткнется на неподвижный упор и остановит вращение главного приводного колеса.

Рассмотрим принцип работы калькулятора Лейбница на примере умножения 10456 на 472:

1. С помощью циферблатов вводится множимое (10456).

2. Устанавливается штифт в среднюю часть вспомогательного счетчика, напротив цифры 2, нанесенной на наружную часть вспомогательного счетчика.

3. Поворачивают главное приводное колесо по часовой стрелки, пока штифт, вставленный в вспомогательный счетчик, не упрется в упор (два поворота).

4. Сдвигается подвижная часть калькулятора Лейбница на одно деление влево, используя вспомогательное приводное колесо.

5. Устанавливается штифт в среднюю часть вспомогательного счетчика, напротив цифры, соответствующей количеству десяток множителя (7).

6. Поворачивается главное приводное колесо по часовой стрелки, пока штифт, вставленный в вспомогательный счетчик, не упрется в упор (семь поворотов).

7. Подвижная часть калькулятора Лейбница сдвигается еще на одно деление влево.

8. Устанавливается штифт в среднюю часть вспомогательного счетчика, напротив цифры, соответствующей количеству сотен множителя (4).

9. Поворачивают главное приводное колесо по часовой стрелки, пока штифт, вставленный в вспомогательный счетчик, не упрется в упор (четыре поворота).

10. Число, появившиеся в окошках отображения результата, – искомое произведение 10456 на 472 (10456 х 472 = 4 935 232).

При делении, сначала, в калькулятор Лейбница вводится делимое с помощью циферблатов, и один раз поворачивается главное приводное колесо по часовой стрелке. Затем, с помощью циферблатов вводится делитель, и главное приводное колесо начинает вращаться против часовой стрелки. При этом результат деления – это количество оборотов главного приводного колеса, а в окошках отображения результатов индицировался остаток от деления.

Если делимое много больше делителя, то для ускорения деления используют сдвиг делителя на необходимое количество разрядов влево с помощью вспомогательного приводного колеса. При этом, во время подсчета количества оборотов главного приводного колеса, необходимо учитывать сдвиг (один оборот главного приводного колеса при сдвиге подвижной части калькулятора Лейбница на одну позицию влево приравнивается к десяти оборотам главного приводного колеса).

Рассмотрим принцип работы калькулятора Лейбница на примере деления 863 на 64:

1. С помощью циферблатов вводим делимое (863).

2. Поворачиваем ручку главного приводного колеса по часовой стрелки один раз.

3. С помощью циферблатов вводим делитель (863).

4. Сдвигаем движущуюся часть калькулятора Лейбница на одну позицию влево с помощью вспомогательного приводного колеса.

5. Поворачиваем главное приводное колесо один раз против часовой стрелки и получаем первую часть результата деления — количество оборотов главного приводного колеса, умноженное на разрядность (положение подвижной части калькулятора). Для нашего случая — это 1х10. Таким образом, первая часть результата деления будет равна 10. В окошках результата отобразится остаток от первой операции деления (223).

6. Сдвигаем движущуюся часть калькулятора Лейбница на одну позицию вправо с помощью вспомогательного приводного колеса.

7. Поворачиваем главное приводное колесо против часовой стрелки до тех пор, пока остаток, отображающийся в окошках результата, не станет меньше делителя. Для нашего случая — это 3 оборота. Таким образом, вторая часть результата будет равна 3. Складываем обе части результата и получаем частное (результат деления) — 13. Остаток от деления отображается в окошках результата и составляет 31.

Сложение осуществляется следующим способом:

1. С помощью установки циферблатов в необходимое положение, вводится первое слагаемое

2. Поворачивается ручка главного приводного колеса по часовой стрелки один раз.

3. Вводится второе слагаемое по той же технологии, как и первое.

4. Еще раз поворачивается ручка главного приводного колеса.

5. В окне результата отображается результат сложения.

Для вычитания необходимо:

1. С помощью установки циферблатов в необходимое положение, вводится уменьшаемое.

2. Поворачивается ручка главного приводного колеса по часовой стрелки один раз.

3. С помощью циферблатов вводится вычитаемое.

4. Поворачивается ручка главного приводного колеса один раз против часовой стрелки.

5. В окне результата отображается результат вычитания.

Несмотря на то, что о машине Лейбница было известно в большинстве стран Европы, она не получила большого распространения из-за высокой себестоимости, сложности изготовления и ошибок, изредка возникающих при переносе разрядов переполнения. Но основные идеи — ступенчатый валик и сдвиг множителя, позволяющие работать с многоразрядными числами, оставили заметный след в истории развития вычислительной техники.

Идеи, изложенные Лейбницем, имели большое количество последователей. Так, в конце 18 века над усовершенствованием калькулятора работали Вагнер и механик Левин, а после смерти Лейбница – математик Тоблер. В 1710 году машину, аналогичную калькулятору Лейбница, построил Буркхардт. Усовершенствованием изобретения занимались и Кнутцен, и Мюллер, и другие выдающиеся ученые того времени.

Арифмометр Лейбница: история создания, особенности, описание, фото

Одним из величайших изобретений XVII века стало создание немецким математиком Готфридом Вильгельмом Лейбницем арифмометра (фото приводится в статье), способного совершать в десятичной системе все четыре основных математических действия. Именно этот вычислительный аппарат можно в полной мере назвать прообразом современного калькулятора.

Юный гений

Будущий изобретатель родился 1 июля 1646 года в Лейпциге и уже в возрасте 14 лет поступил в университет родного города, где изучал гуманитарные науки – историю, философию и юриспруденцию. Вспоминая об этом периоде своей жизни, ученый всегда подчеркивал, что знакомство с трудами выдающихся мыслителей прошлого развило в нем способность творчески подходить к решению сугубо технических проблем, избегая при этом повторения путей, пройденных ранее иными исследователями.

Математикой Лейбниц серьезно занялся лишь двумя годами позже, покинув Лейпциг и став студентом Йенского университета. Посещая лекции своего выдающегося современника – немецкого математика Эрхарда Вайгеля – он, тем не менее, продолжал занятия юриспруденцией и в 17-летнем возрасте опубликовал несколько собственноручно написанных трактатов.

На пути к изобретению

Толчком к созданию Готфридом Лейбницем арифмометра послужила его встреча с голландским астрономом Христианом Гюйгенсом, которому по роду его занятий, постоянно приходилось выполнять громоздкие и весьма сложные математические вычисления. Желая помочь своему новому знакомому, гениальный немец и задался целью изобрести некое механическое устройство, способное взять на себя этот рутинный труд.

Создавая механический арифмометр, Лейбниц имел возможность опираться на опыт своего предшественника – французского ученого Блеза Паскаля, который к тому времени уже изобрел весьма примитивную счетную машину и даже пытался, хотя и безуспешно, наладить ее коммерческое производство. Заметим попутно, что француза побудило к этому желание помочь своему отцу, занимавшемуся сбором налогов и постоянно обремененному множеством вычислений.

Презентация нового арифмометра

Во многом переработав и усовершенствовав счетный аппарат Паскаля, немецкий математик в 1673 году представил общественности Германии совершенно новую модель арифметического устройства, заявив при этом, что намерен и далее продолжать работу над ней. В отличие от своего французского коллеги, конструируя арифмометр, Лейбниц использовал в нем особое ступенчатое колесо, позволяющее упростить и во многом ускорить многократные сложения чисел, необходимые для выполнения операций, связанных с умножением и делением. Были внесены также и некоторые другие усовершенствования, позволявшие автоматически совершать этот процесс.

В последующий период изобретатель вел упорную работу по модернизации своего детища, после чего организовал его презентацию перед членами Лондонского королевского научного общества. Она состоялась в марте 1676 года. Создание арифмометра Лейбница — усовершенствованного и позволявшего без особого труда совершать сложные математические вычисления — стало событием, интерес к которому уже тогда был проявлен во многих европейских странах.

Завершение работы над изобретением

Не останавливаясь на достигнутом и продолжая совершенствовать свой арифмометр, Готфрид Лейбниц в середине 90-х годов представил публике его обновленную модель, которая и стала классическим образцом, вошедшим впоследствии во все справочники мира и получившим имя своего создателя.

Любопытно, что одна из созданных им счетных машин позже была привезена в Россию и попала к Петру I, являвшемуся, как известно, большим любителем и ценителем разных диковинок. Однако на берегах Невы она долго не задержалась и была передана государем в дар китайскому императору как свидетельство необычайного технического прогресса, достигнутого Европой.

Дальнейшие же работы по усовершенствованию своего изобретения ученый вел вплоть до 1710 года, после чего вынужден был прервать их из-за крайне высоких накладных расходов. Достаточно сказать, что в те времена, когда Лейбниц изобрел арифмометр, годовой оклад министра не превышал 2 тыс. талеров, тогда как математик вложил в свое детище сумму в 12 раз большую. Окончательная модель была создана им в двух экземплярах, из которых до настоящего времени сохранился лишь один, представленный в экспозиции Мюнхенского национального музея.

Особенности новой конструкции

Как упоминалось выше, кардинальным отличием созданного Лейбницем арифмометра от разработок, сделанных Паскалем, является наличие в нем ступенчатого вала − особого цилиндра, снабженного по бокам зубцами различного размера. Это приспособление избавляло от необходимости при умножении многократно набирать множимое число. Для получения ответа достаточно было лишь повернуть рукоять, приводящую цилиндр в движение, нужное количество раз. Даже если приходилось умножать большие числа и производимая операция занимала много времени, то и в этом случае преимущество перед арифмометром Паскаля не вызывало сомнения. В конструкцию были введены также и иные элементы, позволяющие упростить и ускорить вычислительный процесс.

Этапы научной деятельности

Рассказывая об арифмометре Лейбница, нельзя не упомянуть и об остальных заслугах этого гениального ученого, осуществившего на рубеже XVII и XVIII веков мощный прорыв в самых различных областях математики. Так, начав в 1667 году службу при дворе Мейнцкого курфюрста, он посвятил много времени созданию основ математического анализа, осуществлявшегося им на иных принципах, чем те, что были сформулированы Ньютоном. Тогда же Лейбницем был написан и капитальный научный труд, в котором он изложил разработанные им основы дифференциального исчисления.

Настоящей революцией в математике стала введенная Лейбницем в середине 80-х годов классификация вещественных чисел, при которых они подразделялись на трансцендентные и алгебраические. То же ему удалось проделать и при изучении кривых линий. Кроме того, в число наиболее значимых достижений ученого вошло введение им в математику такого понятия, как интеграл, которым он обозначил операцию, противоположную дифференцированию.

Параллельно с разработкой арифмометра, Лейбниц занимался и вопросами, входящими в круг линейной алгебры. Однако результаты его работ были по достоинству оценены лишь спустя полвека. Исследуя линейные системы, он ввел в науку неизвестное до той поры понятие «определителя», которое тогда прошло незамеченным в научных кругах, но со временем умножило его славу. Как бы это ни показалось удивительным, но Готфриду Лейбницу принадлежит вклад и в создание современной компьютерной техники. Именно он, оперируя значениями нуля и единицы, разработал широко используемую сегодня двоичную систему исчисления.

Роль Лейбница в истории Германии

Достижения ученого, ушедшего из жизни в 1716 году, во многом помогли Германии не только сделать значительный шаг в своем техническом развитии, но и преодолеть тот экономический и политический упадок, в котором она находилась после поражения в Тридцатилетней войне, охватившей Европу в период 1618-1648 гг.