Операционные устройства вычислительных машин

Операционные устройства ЭВМ

В классической фон-неймановской ВМ функция арифметической и логической обработки данных возлагается на арифметико-логическое устройство (АЛУ). Учитывая разнообразие выполняемых операций и типов обрабатываемых данных, реально можно говорить не о едином устройстве, а о комплексе специализированных операционных устройств (ОПУ), каждое из которых реализует определенное подмножество арифметических или логических операций, предусмотренных системой команд ВМ. С этих позиций следует выделить:

— ОПУ целочисленной арифметики;

— ОПУ для реализации логических операций;

— ОПУ десятичной арифметики;

— ОПУ для чисел с плавающей запятой.

На практике две первых группы обычно объединяются в рамках одного операционного устройства. Специализированные ОПУ десятичной арифметики в современных ВМ встречаются достаточно редко, поскольку обработку чисел, представленных в двоично-десятичной форме, можно достаточно эффективно организовать на базе средств целочисленной двоичной арифметики. Таким образом, будем считать, что АЛУ образуют два вида операционных устройств: целочисленное ОПУ и ОПУ для обработки чисел в формате с плавающей запятой (ПЗ).

В минимальном варианте АЛУ должно содержать аппаратуру для реализации, лишь основных логических операций, сдвигов, а также сложения и вычитания чисел в форме с фиксированной запятой (ФЗ). Опираясь на этот набор, можно программным способом обеспечить выполнение остальных арифметических и логических операций как для чисел с фиксированной запятой, так и для других форм представления информации. Следует, однако, учитывать, что подобный вариант не позволяет добиться высокой скорости вычислений, поэтому по мере расширения технологических возможностей доля аппаратных средств в составе АЛУ постоянно возрастает.

Набор элементов, на основе которых строятся структуры различных ОПУ, называется структурным базисом. Структурный базис ОПУ включает в себя:

— регистры, обеспечивающие кратковременное хранение слов данных;

— управляемые шины, предназначенные для передачи слов данных;

— комбинационные схемы, реализующие вычисление функций микроопераций и логических условий по управляющим сигналам от устройства управления.

С практических позиций больший интерес представляют два вида структур ОПУ: жесткая и магистральная.

В ОПУ с жесткой структурой комбинационные схемы жестко распределены между всеми регистрами. К каждому регистру относится свой набор комбинационных схем, позволяющих реализовать определенные микрооперации. Достоинством ОПУ с жесткой структурой является высокое быстродействие, недостатком – малая регулярность структуры, что затрудняет реализацию таких ОПУ в виде больших интегральных схем.

В ОПУ с магистральной структурой все внутренние регистры объединены в отдельный узел регистров общего назначения (РОН), а все комбинационные схемы – в операционный блок (ОПБ), который зачастую ассоциируют с термином «арифметико-логическое устройство». Операционный блок и узел регистров сообщаются между собой с помощью магистралей – отсюда и название «магистральное ОПУ».

Пример магистрального ОПУ представлен на рис. 2.6.

Рис. 2.6. Структура магистрального ОПУ

В состав узла РОН здесь входят N регистров общего назначения, подключаемых к магистралям А и В через мультиплексоры MUX А и MUX В. Каждый из мультиплексоров является управляемым коммутатором, соединяющим выход одного из РОН с соответствующей магистралью. Номер подключаемого регистра определяется адресом a или b, подаваемым на адресные входы мультиплексора из устройства управления.

В операционных устройствах для обработки чисел с плавающей запятой вместо РОН часто используется отдельный узел регистров с плавающей запятой.

По магистралям А и В операнды поступают на входы операционного блока, к которым подключается комбинационная схема, реализующая требуемую микрооперацию (по сигналу управления из УУ). Таким образом, любая микрооперация ОПБ может быть выполнена над содержимым любых регистров ОПУ. Результат микрооперации по магистрали С заносится через демультиплексор DMX С в конкретный регистр узла РОН. Демультиплексор представляет собой управляемый коммутатор, имеющий один информационный вход и N информационных выходов. Вход подключается к выходу с заданным адресом «с», который поступает на адресные входы DMX С из УУ.

Основным достоинством магистральных ОПУ является высокая универсальность и регулярность структуры, что облегчает их реализацию на кристаллах интегральных схем (ИС). Вообще говоря, магистральная структура ОПУ в современных ЭВМ является превалирующей.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Глава 7.

Операционные устройства вычислительных машин

— ОПУ целочисленной арифметики;

— ОПУ для реализации логических операций;

— ОПУ десятичной арифметики;

— ОПУ для чисел с плавающей запятой.

В минимальном варианте АЛУ должно содержать аппаратуру для реализации лишь основных логических операций, сдвигов, а также сложения и вычитания чисел в форме с фиксированной запятой (ФЗ). Опираясь на этот набор, можно программным способом обеспечить выполнение остальных арифметических и логических операций как для чисел с фиксированной запятой, так и для других форм представления информации. Следует, однако, учитывать, что подобный вариант не позволяет добиться высокой скорости вычислений, поэтому по мере расширения технологических возможностей доля аппаратных средств в составе АЛУ постоянно возрастает.

Порядок следования целевых функций полностью определяет динамику работы устройства управления и всей ВМ в целом. Этот порядок удобно задавать и отображать в виде граф-схемы этапов исполнения команды (ГСЭ). Как и граф-схема микропрограммы, ГСЭ содержит начальную, конечную, операторные и условные вершины. В начальной и конечной вершинах проставляется условное обозначение конкретной команды, а в условной вершине записывается логическое условие, влияющее на порядок следования этапов. В операторные вершины вписываются операторы этапов.

По форме записи оператор этапа — это оператор присваивания, в котором:

— слева от знака присваивания указывается наименование результата действий, выполненных на этапе;

— справа от знака присваивания записывается идентификатор целевой функции определяющей текущие действия, а за ним (в скобках) приводится список исходных данных этапа.

Исходной информацией для первого этапа служит хранящийся в счетчике команд адрес А_ki, текущей команды К_i. Процесс выборки команды отображается оператором первого этапа: К_i:= BK(A_Kj).

Адрес А_ki, обеспечивает также второй этап, результатом которого является адрес следующей команды А_ki₊₁, поэтому оператор второго этапа имеет вид: A_Ki₊₁ := ФАСК(А_ki). В качестве исходных данных для третьего этапа машинного цикла выступают содержащиеся в коде текущей команды способ адресации CA_i (он определяет конкретную модификацию ЦФ-ФИАО) и код адресной части А_i. Результатом становится исполнительный адрес операнда А_исп := ФИА(С_А_i, А_i).

Полученный адрес используется на четвертом этапе для выборки операнда

Результат исполнения операции P0_j, получаемый на пятом этапе машинного цикла, зависит от кода операции 2-й команды K0n_i (определяет модификацию ЦФ-ИО), кода первого операнда O_i и кода второго операнда — результата предыдущей (i-1)-й операции РО_i_-1: РО_i := ИО(Коп_i, О_i, РО_i_-1).

В соответствии со структурой граф-схемы этапов все команды ВМ можно разделить на три типа:

— команды типа «Сложение» (Сл);

— команды типа «Запись» (Зп);

— команды типа «Условный переход» (УП).

Типовые граф-схемы этапов представлены на рис. 6.1.

Видно, что количество этапов в командах типа «Сл» (см. рис. 6.1, а) колеблется от трех (для непосредственной адресации НА) до пяти. При непосредственной адресации второй операнд записан в адресной части команды, поэтому нет необходимости в реализации устройством управления целевых функций ЦФ-ФИ А, ЦФ-ВО. Количество этапов для команд типа «Зп» постоянно и равно четырем (см. рис. 6.1, б) здесь отсутствует необходимость в ЦФ-ВО. Машинный цикл команд типа «УП» состоит из трех этапов (см. рис. 6.1, в), поскольку здесь, помимо выборки операнда, можно исключить и этап ФАСК — действия, обычно выполняемые на этом этапе, фактически реализуются на этапе ИО.

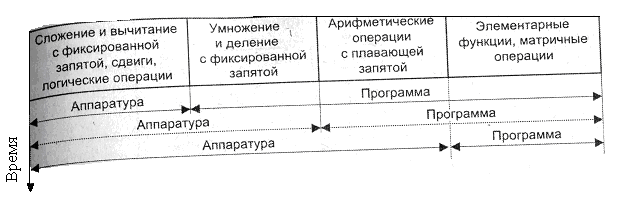
Рис 7.1 • Динамика изменения соотношения между аппаратной и программной реализациями

На рис. 7.1 показана динамика изменения соотношения между аппаратной и программной реализациями функций АЛУ по мере развития элементной базы вычислительной техники. Здесь подразумевается, что по вертикальной оси откладывается календарное время.

Тема 9. Операционные устройства вычислительных машин.

Структуры операционных устройств. Операционные устройства с жесткой структурой. Операционные устройства с магистральной структурой. Алгоритм SRT. Операционные устройства с плавающей запятой. Реализация логических операций.

Тема 10. Организация памяти вычислительных систем.

Память с чередованием адресов. Модели архитектуры памяти вычислительных систем. Модели архитектур распределенной памяти. Мультипроцессорная когерентность кэш-памяти. Аппаратные способы решения проблемы когерентности.

Тема 11. Топологии вычислительных систем. Потоковые и редукционные вычислительные системы.

Метрики сетевых соединений. Функции маршрутизации данных. Статические топологии. Линейная топология. Кольцевые топологии. Звездообразная топология. Древовидные топологии. Решетчатые топологии. Полносвязная топология. Топология гиперкуба. Шинная топология. Топология перекрестной коммутации. Топология базовой линии.

Вычислительные системы с управлением вычислениями от потока данных. Вычислительная модель потоковой обработки. Архитектура потоковых вычислительных систем. Статические потоковые вычислительные системы. Динамические потоковые вычислительные системы. Макропотоковые вычислительные системы. Вычислительные системы с управлением вычислениями по запросу.

Тема 12.Методологические основы развития науки об управлении.

Охватывается круг вопросов, связанных с изложением методологических основ развития науки об управлении, как точной науки, которая опирается на конкретное знание. Рассматриваются общие разделы, дается характеристика разновидностей современных систем управления и принципов их классификаций, теории адаптивного управления; теории интеллектуальных систем и различных видов задач системного анализа.

Основная литература

1. Основная литература

1. Булдаков, С.К. История и философия науки: Учеб. пособие для аспирантов и соискателей учёной степени кандидата наук. — М.: РИОР, 2008. — 141с. — Высшее образование: http://znanium.com/bookread.php?book=141950

2. Цилькер Б.Я. Организация ЭВМ и систем: Учебник для вузов / Б.Я. Цилькер, С.А. Орлов. — 2-е изд. — СПб.: Питер, 2011. — 688 с.

3. Степанов А.Н.Архитектура вычислительных систем и компьютерных сетей:Учебник / СПб: Питер, 2007. — 509с.

4. Концепции современного естествознания: Учебник / В.М. Найдыш. — 3-e изд., перераб. и доп. — М.: Альфа-М: ИНФРА-М, 2007. — 704 с.: http://znanium.com/bookread.php?book=123452

5. Курс лекций по специальному курсу «История науки и техники». Под общ.ред. Бодровой Е.В., Гусаровой М.Н. — М.:МГАПИ, 2006. — 100 с.

6. Авдеев В.А. Периферийные устройства: интерфейсы, схемотехника, программирование. — М.: ДМК Пресс, 2009.

Гук М.Ю. Аппаратные средства IBM PC. Энциклопедия. 3-е изд. — СПб.: Питер, 2006.

Заславская О.Ю., Кравец, О.Я., Говорский А.Э. Архитектура компьютера и вычислительных систем (лекции, лабораторные работы, контрольные задания): Учебник/О.Ю. Заславская, О.Я. Кравец, А.Э. Говорский; под ред. чл.-корр.РАО, д-ра техн. наук профессора С.Г. Григорьева. – Воронеж: «Научная книга», 2011. – 300 с.

Заславская О.Ю., Левченко И.В. Архитектура компьютера. // В сб.: Типовые программы по информатике и прикладной математике для студентов и преподавателей педагогических университетов. / Под ред. С.Г. Григорьева. – М.: МГПУ, 2006. – С.14-18.

Кравец О.Я. Практикум по вычислительным сетям и телекоммуникациям: Учеб. пособие. — Изд. 4-е, исправл. — Воронеж: Научная книга, 2009.

Кравец О.Я. Сети ЭВМ и телекоммуникации: Учеб. пособие. — Воронеж: «Научная книга», 2010.

Кравец О.Я., Подвальный Е.С., Титов В.С., Ястребов А.С. Архитектура вычислительных систем с элементами конвейерной обработки: Учеб. пособие. – СПб.: Политехника, 2009.

Кравец О.Я., Подвальный Е.С., Толпинская Н.Б., Садовой Н.Н. Вычислительные комплексы и системы: компоненты, технологии, реализация: Учеб.пособие. — Ростов н/Д: Издательский центр ДГТУ, 2007.

Кравец О.Я., Сафонов А.И. Методология анализа и проектирования специализированных многозвенных клиент-серверных систем. — Воронеж: «Научная книга», 2010.

Таненбаум Э. Архитектура компьютеров. — СПб.: Питер, 2007.

Хульцебош Ю. USB в электронике. — СПб.: Питер, 2009.

Операционные устройства вычислительных машин

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Операционные устройства вычислительных машин

— ОПУ целочисленной арифметики;

— ОПУ для реализации логических операций;

— ОПУ десятичной арифметики;

— ОПУ для чисел с плавающей запятой.

Порядок следования целевых функций полностью определяет динамику работы устройства управления и всей ВМ в целом. Этот порядок удобно задавать и отображать в виде граф — схемы этапов исполнения команды (ГСЭ). Как и граф-схема микропрограммы, ГСЭ содержит начальную, конечную, операторные и условные вершины. В начальной и конечной вершинах проставляется условное обозначение конкретной команды, а в условной вершине записывается логическое условие, влияющее на порядок следования этапов. В операторные вершины вписываются операторы этапов.

По форме записи оператор этапа — это оператор присваивания, в котором:

— слева от знака присваивания указывается наименование результата действий, выполненных на этапе;

Исходной информацией для первого этапа служит хранящийся в счетчике команд адрес А ki , текущей команды К i . Процесс выборки команды отображается оператором первого этапа: К i := BK(A Kj ).

Адрес А ki , обеспечивает также второй этап, результатом которого является адрес следующей команды А ki +1 , поэтому оператор второго этапа имеет вид: A Ki +1 := ФАСК(А ki ). В качестве исходных данных для третьего этапа машинного цикла выступают содержащиеся в коде текущей команды способ адресации CA i (он определяет конкретную модификацию ЦФ-ФИАО) и код адресной части А i . Результатом становится исполнительный адрес операнда А исп := ФИА(С А i , А i ).

Полученный адрес используется на четвертом этапе для выборки операнда

Результат исполнения операции P0 j , получаемый на пятом этапе машинного цикла, зависит от кода операции 2-й команды K0n i (определяет модификацию ЦФ-ИО), кода первого операнда O i и кода второго операнда — результата предыдущей (i-1)-й операции РО i -1 : РО i := ИО(Коп i , О i , РО i -1 ).

В соответствии со структурой граф-схемы этапов все команды ВМ можно разделить на три типа:

— команды типа «Сложение» (Сл);

— команды типа «Запись» (Зп);

— команды типа «Условный переход» (УП).

Типовые граф — схемы этапов представлены на рис. 6.1.

Видно, что количество этапов в командах типа «Сл» (см. рис. 6.1, а) колеблется от трех (для непосредственной адресации НА) до пяти. При непосредственной адресации второй операнд записан в адресной части команды, поэтому нет необходимости в реализации устройством управления целевых функций ЦФ-ФИ А, ЦФ-ВО. Количество этапов для команд типа «Зп» постоянно и равно четырем (см. рис. 6.1, б) здесь отсутствует необходимость в ЦФ-ВО. Машинный цикл команд типа «УП» состоит из трех этапов (см. рис. 6.1, в), поскольку здесь, помимо выборки операнда, можно исключить и этап ФАСК — действия, обычно выполняемые на этом этапе, фактически реализуются на этапе ИО.

Рис 7.1 • Динамика изменения соотношения между аппаратной и программной реализациями

Структуры операционных устройств

— регистры, обеспечивающие кратковременное хранение слов данных;

— управляемые шины, предназначенные для передачи слов данных;

— комбинационные схемы, реализующие вычисление функций микроопераций

и логических условий по управляющим сигналам от устройства управления.

Используя методику, изложенную в [21], можно синтезировать ОПУ с так называемой канонической структурой, являющуюся основополагающей для синтеза других структур. Такая структура образуется путем замены каждого элемента реализуемой функции соответствующим элементом структурного базиса. Каноническая структура имеет максимальную производительность по сравнению с другими вариантами структур, однако по затратам оборудования является избыточной. С практических позиций больший интерес представляют два иных вида структур ОПУ: жесткая и магистральная.

Операционные устройства с жесткой структурой

В ОПУ с жесткой структурой комбинационные схемы жестко распределены между всеми регистрами. К каждому регистру относится свой набор комбинационных схем, позволяющих реализовать определенные микрооперации. Пример ОПУ Жесткой структурой, обеспечивающего выполнение операций типа «сложение», приведен на рис. 7.2.

В состав ОПУ входят три регистра со своими логическими схемами:

— регистр первого слагаемого РСл1 и схема ЛРСл1;

— регистр второго слагаемого РСл2 и схема ЛРСл2;

— регистр суммы РСм и схема комбинационного сумматора См.

Рис. 7.2. Операционное устройство с жесткой структурой

Логическая схема Л РСл2 реализует микрооперации передачи второго слагаемого из РСл2 на левый вход сумматора:

— прямым кодом ЛСм := РСл2 (по сигналу управления ВхРСл2);

— инверсным кодом ЛСм := ->РСл2 (по сигналу управления В 1 -РСлЗ);

— со сдвигом на один разряд влево ЛСм := 1Л(РСл2 • 0) (по сигналу управлений

Логическая схема ЛРСл1 обеспечивает передачу результата из регистра РСм

— прямым кодом РСл1 := РСм (по сигналу управления ПгРСл1);

— со сдвигом на один разряд влево РСл1 :=L1(РСм .0) (по сигналу управления L1РСм)

— со сдвигом на два разряда вправо РСл1 := R2(s • s • РСм) (по сигналу управления R1PCм).

Комбинационный сумматор См предназначен для суммирования (обычного или

по модулю 2) операндов, поступивших на его левый (ЛСм) и правый (ПСм) входы.

Результат суммирования заносится в регистр РСм: РСм := ЛСм + ПСм (по сигналу

управления П2РСм) или РСм := ЛСм © ПСм (по сигналу управления П2М2РСм).

Моделью ОПУ с жесткой структурой является так называемый I-автомат,

с особенностями синтеза которого можно ознакомиться в [21, 25].

Аппаратные затраты па ОПУ с жесткой структурой Сж можно оценить по вы-

где N — количество внутренних слов ОПУ; n 1 . п N — длины слов; n = (n 1+ . n N )

— средняя длима слова; k ij . — количество микроопераций типа j =1,2. К (сложе

ние, сдвиг, передача и т. п.), используемых для вычислений слов с номерами

i=1,2,…,N; Ст — цена триггера; Cj — цена одноразрядной схемы для реализации микрооперации j-ro типа.

В приведенном выражении первое слагаемое определяет затраты на хранен

n-разрядных слов, второе — на связи регистров с комбинационными схемами,

а третье — суммарную стоимость комбинационных схем, реализующих микрооперации К типов над N словами.

Затраты времени на выполнение операций типа «сложение» в ОПУ с жесткой структурой равны

где t в — длительность микрооперации выдачи операндов из регистров; t с — продолжительность микрооперации «сложение»; t п — длительность микрооперации приема результата в регистр.

Достоинством ОПУ с жесткой структурой является высокое быстродействие, недостатком — малая регулярность структуры, что затрудняет реализацию таких ОПУ в виде больших интегральных схем.

Операционные устройства с магистральной структурой

В ОПУ с магистральной структурой все внутренние регистры объединены в отдельный узел регистров общего назначения (РОН)’, а все комбинационные схемы— в операционный блок (ОПБ), который зачастую ассоциируют с термином

Операционный блок и узел регистров сообщаются между собой с помощью

магистралей — отсюда и название «магистральное ОПУ».

Пример магистрального ОПУ представлен на рис. 7.3.

Рис. 7.3. Магистральное операционное устройство

В состав узла РОН здесь входят N регистров общего назначения, подключаемых к магистралям А и В через мультиплексоры MUX А и MUX В. Каждый из мультиплексоров является управляемым коммутатором, соединяющим выход одного из РОН с соответствующей магистралью. Номер подключаемого регистра определяется адресом а или Ь, подаваемым на адресные входы мультиплексора из устройства управления.

В операционных устройствах для обработки чисел с плавающей запятой вместо РОН часто используется отдельный узел регистров с плавающей занятой.

По магистралям А к В операнды поступают на входы операционного блоки, к которым подключается комбинационная схема, реализующая требуемую микрооперацию (по сигналу управления из УУ). Таким образом, любая микрооперация ОПБ может быть выполнена над содержимым любых регистров ОПУ. Результат микрооперации по магистрали С заносится через демультпплексор DMX С и конкретный регистр узла РОН. Демультиплексор представляет собой управляемый коммутатор, имеющий один информационный вход и N информационных выходов.

Вход подключается к выходу с заданным адресом с, который поступает на адресные входы DMX С из УУ.

Моделью 0ПУ с магистральной структурой является М-автомат. М-автоматом

называется модель ОПУ, построенная па основе принципа объединения комбинационных схем и реализующая а каждом такте только одну микрооперацию. Синтез М-автоматов рассматривается и [22].

И
спользуя обозначения, введенные в предыдущем разделе, выражение для оценки аппаратных затрат на магистральное ОПУ можно записать в следующем виде:

где первое слагаемое определяет затраты на N регистров, второе — затраты на связи узла РОН и ОПБ, а третье — суммарную цену ОПБ.

Из сопоставления выражении для затрат следует, что магистральная структура экономичнее жесткой структуры, если

где —
количество микроопераций, реализуемых ОПУ с жесткой структурой.

С учетом последнего неравенства можно сформулировать следующее сильней

условие экономичности магистральных структур:

Затраты времени на сложение в магистральных ОПУ больше, чем в ОПУ с жесткой структурой:

где tмих – задержка на подключение операндов из РОН к ОПБ; t DMX — задержи

на подключение результата к РОН.

Основным достоинством магистральных ОПУ является высокая универсальность и регулярность структуры, что облегчает их реализацию на кристаллах ИС. Вообще говоря, магистральная структура ОПУ в современных ВМ является превалирующей.

Классификация операционных устройств с магистральной структурой

Магистральные ОПУ классифицируют по виду и количеству магистралей, организации узла РОН, типу ОПБ.

Магистрали ОПУ могут быть однонаправленными и двунаправленными, соответственно обеспечивающими передачу данных в одном или двух различных направлениях. Типичным режимом работы магистрали является разделение времени,

при котором магистраль используется для передачи функционально разнотипных

данных в различные моменты времени.

По функциональному назначению выделяют:

— магистрали «внешних связей, соединяющих ОПУ с памятью и каналами ввода/

— внутренние магистрали ОПУ, отвечающие за связь между узлом РОН и операционным блоком.

Количество магистралей внешних связей зависит от архитектуры конкретной ВМ и обычно не превышает двух для внешних связей и трех — для внутренних.

Структура трехмагистрального ОПУ представлена на рис. 7.4, а), а соответствующая ему микропрограмма выполнения операции типа «сложение» — на рис. 7.4, б).

Рис. 7.4. Трехмагистральное ОПУ: а — структура; б — микропрограмма сложения

Данный вариант характеризуется наибольшим быстродействием: выборка операндов из РОН, выполнение микрооперации суммирования и запись результата

в РОН — все эти действия производятся за один такт. Основной недостаток трех-

магистральной организации — большая площадь, занимаемая магистралями на кристалле БИС (от 0,16 до 0,22 от площади кристалла).

Двухмагистральная организация при меньшей площади, покрываемой магистралями (от 0,06 до 0,19 от площади кристалла), требует введения как минимум одного буферного регистра (БР), предназначенного для временного хранения одного из операндов (рис. 7.5, а), при этом операция сложения будет выполняться уже за два такта (рис. 7.5, б):

— Такт 1: загрузка БР одним из операндов.

— Такт 2: выполнение микрооперации в ОПБ над содержимым БР и одного из

РOH; запись результата в РОН.

Наконец, организация ОПУ на основе только одной магистрали (рис. 7.6, а)

минимизирует расходы площади (от 0,03 до 0,09 от площади кристалла).

В одномагистральном ОПУ, вместе с тем, возникает необходимость введения не менее двух буферных регистров БР1. БР2. и длительность операции возрастает

до трех тактов (рис. 7.6, б):

Рис, 7.5. Двухмагистральное ОПУ: а — структура; б — микропрограмма сложения

Рис. 7.6. Одномагистральное ОПУ: а — структура; б — микропрограмма сложения

— Такт 1: загрузка БР1 одним из операндов.

— Такт 2: загрузка БР2 вторым операндом.

— Такт З: выполнение микрооперации в ОГЩ над содержимым БР1 и БР2; запись результата в один из РОН.

Организация узла РОН магистрального операционного устройства

Количество регистров в узле РОН магистрального ОПУ обычно превышает тот минимум, который необходим для реализации универсальной системы операций. Избыток регистров используется:

— для хранения составных частей адреса (индекса, базы);

— в качестве буферной, сверхоперативной памяти для повышения производительности ВМ за счет уменьшения требуемых пересылок между основной памятью и ОПУ.

Количество регистров колеблется в среднем от 8 до 16, иногда может достигав 32-64. В процессорах с сокращенным набором команд количество РОН доходит до нескольких сотен. 1

Организация узла РОН может обеспечивать одноканальный или двухканальный доступ как по входу (записи), так и по выходу (считыванию). В первом случае

В входу узла подключается один демультиплексор, а к выходу — один мультиплексор. Во втором случае доступ осуществляется с помощью двух демулътиплексоров и (или) двух мультиплексоров. Двухканальный доступ повышает быстродействие 0ПУ- так как позволяет обратиться параллельно к двум регистрам.

Организация операционного блока магистрального операционного устройства

Тип операционного блока (ОПБ) определяется способом обработки данных. Различают ОПБ последовательного и параллельного типа.

В последовательном операционном блоке (рис. 7.7) операции выполняются побитово, разряд за разрядом.

Рис. 7,7. Последовательный операционный блок

Бит переноса, возникающий при обработке 1-го разряда операндов, подается на вход ОПБ и учитывается при обработке (i+1)-го разряда операндов. Результат побитово заносится в выходной регистр, предыдущее содержимое которого перед этим сдвигается па один разряд. Таким образом, после n циклов в выходном регистре формируется слово результата, где каждый разряд занимает предназначенную для него позицию.

При параллельной организации операционного блока (рис. 7.8) всё разряды операндов обрабатываются одновременно. Внутренние переносы обеспечиваются схемой ОПБ. Более подробно возможности организации переносов рассматриваются позже.

Рис. 7.8. Параллельный операционный блок

Микрооперация П i обеспечивает передачу результата на магистраль С без сдвига. Пo ходу микрооперации R, результат сдвигается на один разряд вправо, при этом в освобождающийся старший разряд заносится значение с внешнего контакта SL, а выдвигаемый (младший) разряд сумматора посылается внешний контакт 5R.

В микрооперации L, результат сдвигается на один разряд влево. Здесь в освобождающийся младший разряд заносится значение с внешнего контакта SR, а выдвигаемый (старший) разряд См передается на внешний контакт SL.

Базис целочисленных операционных устройств

Для большинства современных ВМ общепринятым является такой формат с фиксированной запятой (ФЗ), когда запятая фиксируется справа от младшего разряда кода числа. По этой причине соответствующие операционные устройства называют целочисленными ОПУ. В форме с ФЗ могут быть представлены как числа без знака, когда все n позиций числа отводятся под значащие цифры, так и со знаком. В последнем случае старшим (n-1)-й разряд числа занимает знак числа (0 —плюс, 1 — минус), а под значащие цифры отведены разряды с (n- 2)-го по 0-й.

При записи отрицательных чисел используется дополнительный код, который для числа N получается по следующей формуле:

Если исключить логические операции, которые рассматриваются отдельно, целочисленное ОПУ должно обеспечивать выполнение следующих арифметических

операций над числами без знака и со знаком:

Сложение и вычитание

На рис. 7.10 приводятся примеры сложения целых чисел, представленных в дополнительном коде (напомним, что при сложении в дополнительном коде знаковый разряд участвует в операции наравне с цифровыми).

Рис. 7,10. Примеры выполнения операции сложения в дополнительном коде:

а, б, в, г — сложение без возникновения переполнения;

д, е — сложение с переполнением

При сложении — разрядных двоичных чисел (бит знака и n-1 значащих цифр)

возможен результат, содержащий n значащих цифр. Эта ситуация известна как переполнение. «Лишний» бит занимает позицию знака, что приводит к некорректности результата. Естественно, что ОПУ должно обнаруживать факт переполнения и сигнализировать о нем. Для этого используется следующее правило: ее»-

суммируются два числа и они оба — положительные или оба отрицательные, Переполнение имеет место тогда и только тогда, когда знак результата противоположен знаку слагаемых. Рисунки 7.10,3 и 7.10, е показывают примеры переполнения, Обратим внимание, что переполнение не всегда сопровождается переносов

из знакового разряда.

Рис. 7.11. Примеры выполнения операции вычитаний в дополнительном коде: а, б, s, г — вычитание без возникновения переполнения; д, е — вычитание с переполнением J

Вычитание выполняется в соответствии с правилом: для вычитания одного числа (вычитаемого) из другого (уменьшаемого) необходимо взять дополнение вычитаемого и прибавить его к уменьшаемому. Под дополнением здесь понимается вычитаемое с противоположным знаком, представленное в дополнительном коде.

Вычитание иллюстрируется примерами (рис. 7.11). Два последних примера (см. рис. 7.11,д и 7.11,е) демонстрируют ранее рассмотренное правило обнаружения переполнения.

Чтобы упростить обнаружение ситуации переполнения, часто применяется так

называемый модифицированный дополнительный код, когда для хранения знака

отводятся два разряда, причем оба участвуют в арифметической операции наравне с цифровыми разрядами. В нормальной ситуации оба знаковых разрядах содержат одинаковые значения. Различие в содержимом знаковых разрядов служит признаком возникшего переполнения (рис. 7.12).

Рис. 7.12. Примеры выполнения операции сложения в модифицированном дополнительном коде: а, б — переполнения нет; в, г — возникло переполнение

На рис. 7.13 показана возможная структура операционного блока для сложения и вычитания чисел со знаком в формате с фиксированной запятой. Центральным звеном устройства является n-разрядный двоичный сумматор. Операнд А поступает на вход сумматора без изменений. Операнд В предварительно пропускается через схемы сложения по модулю 2, поэтому вид кода В, поступающего на другой вход сумматора, зависит от выполняемой операции. Если задана операция сложения (управляющий код 0), то результат на выходе ОПБ определяется выражением S=A+B. При операции вычитания (управляющий код 1) на вход сумматора подаются инверсные значения всех разрядов В, и, кроме того, на вход переноса в младший разряд сумматора С IN поступает 1. В итоге на выходе ОПБ будет S= A + B + 1,что соответствует прибавлению к А числа В с противоположным знаком, то есть вычитанию.

Рис. 7.13. Структура операционного блока для сложения и вычитания

На рис. 7.13 не показана схема формирования признака переполнения V, который согласно описанным ранее правилам определяется логическим выражением

По сравнению со сложением и вычитанием, умножение — более сложная операция, как при программном, так и при аппаратном воплощении. В ВМ применяются различные алгоритмы реализации операции умножения и, соответственно, несколько схем построения операционных блоков, обеспечивающих выполнение операции умножения.

Традиционная схема умножения похожа на известную из школьного курса процедуру записи «в столбик». Вычисление произведения Р двух

n-разрядных двоичных чисел без знака А сводится к формированию частичных произведений (ЧП) W i , по одному на каждую цифру множителя, с последующим суммированием полученных ЧП. Перед суммированием каждое частичное произведение должно быть сдвинуто на один разряд относительно предыдущего согласно весу цифры множителя, которой это ЧП соответствует. Поскольку операндами являются двоичные числа, вычисление

ЧП упрощается — если цифра множителя b i , равна 0, то W i тоже равно 0, а при Ь i =1 частичное произведение равно множимому (W i = А). Перемножение двух n-разрядных двоичных чисел Р=АхВ приводит к получению результата, содержащего

2n битов. Таким образом, алгоритм умножения предполагает последовательное

выполнение двух операций — сложения и сдвига (рис. 7.14). Суммирование ЧП обычно производится не на завершающем этапе, а по мере их получения. Это позволяет избежать необходимости хранения всех ЧП, то есть сокращает аппаратурные издержки. Согласно данной схеме, устройство умножения предполагает наличие регистров множимого, множителя и суммы частичных произведений, а также сумматора ЧП и, возможно, схем сдвига, если операция сдвига не реализована иным способом, например за счет «косой» передачи данных между узлами умножителя.

Рис. 7.14. Общая схема умножения со сдвигом суммы частичных произведений влево или вправо

В зависимости от способа получения суммы частичных произведений (СЧП),

возможны четыре варианта реализации «традиционной» схемы умножения [10|:

1. Умножение, начиная с младших разрядов множителя, со сдвигом суммы частичных произведении вправо п при неподвижном множимом.

2. Умножение, начиная со старших разрядов множителя, при сдвиге суммы частичных произведений влево и неподвижном множимом.

3. Умножение, начиная с младших разрядов множителя, при сдвиге множимого влево и неподвижной сумме частичных произведении.

4. Умножение, начиная со старших разрядов множителя, со сдвигом множимого вправо и при неподвижной сумме частичных произведений.

Варианты со сдвигом множимого на практике не используются, поскольку для их реализации регистр множимого, регистр СЧП и сумматор должны иметь разрядность 2n, поэтому остановимся на вариантах 1 и 2. Первый из них назовем алгоритмом сдвига вправо, а второй — алгоритмом сдвига влево.

Умножение чисел без знака

Общую процедуру традиционного умножения сначала рассмотрим применительно к числам без знака, то есть таким числам, в которых все n разрядов представляют значащие цифры.

Алгоритм сдвига вправо

Алгоритм сводится к следующим шагам:

1. Исходное значение суммы частичных произведений принимается равным нулю.

2. Анализируется очередная цифра множителя (анализ начинается с младшей

цифры). Если она равна единице, то к СЧП прибавляется множимое, в противном случае (цифра равна нулю) прибавление не производится.

3. Выполняется сдвиг суммы частичных произведений вправо па один разряд.

4. Пункты 2 и 3 последовательно повторяются для всех цифровых разрядов множителя.

Процедура умножения иллюстрируется примером вычисления произведения

Рис. 7.15. Пример умножения со сдвигом суммы частичных произведений вправо

Алгоритм может быть реализован с помощью схемы, показанной на рис. 7.16.

Рис. 7.16. Схема устройства умножения по алгоритму правого сдвига

Первоначально множимое и множитель заносятся в n-разрядные регистры множимого (РМн) и множителя (РМт) соответственно, а все разряды 2n-разрядного

регистра суммы частичных произведений (РЧП) устанавливаются в 0. Умножение происходит за n шагов. На каждом шаге, в зависимости от состояния младшего

Разряда регистра множителя, управляющего мультиплексором, на один из входов n-разрядного сумматора подается либо множимое, либо 0. На второй вход поступает содержимое n старших разрядов РЧП. Новое частичное произведение из сумматора пересылается в старшие разряды РЧП. Далее содержимое РЧП сдвигается на один разряд вправо, причем в освободившийся старший разряд регистра заносится значение переноса из старшего разряда сумматора. Поскольку мультиплексор управляется младшим разрядом РМт, то содержимое этого регистра также сдвигается на один разряд вправо. Описанная последовательность повторяется n раз. Более экономичным в плане аппаратуры является иное решение, когда вместо двух регистров — n-разрядного РМт и 2/7-разрядного РЧП — используется один комбинированный 2n-разрядный регистр (показан на рис 7.16 справа). Множитель первоначально заносится в младшие n разрядов этого регистра, а старшие разряды обнуляются. По мере сдвигов вправо младшие, уже проанализированные разряду множителя выталкиваются из регистра, освобождая место для очередной цифры СЧП. Обычно такой регистр строится из двух n-разрядных регистров, объединенных цепями сдвига. Дополнительно отметим, что если очередная цифра множителя равна 1, то для вычисления суммы ЧП требуются операции сложения и сдвига, а при нулевой цифре множителя в принципе можно обойтись без сложения, ограничившись только сдвигом. Это, естественно, требует некоторого видоизменения схемы.

Алгоритм сдвига влево

Процедура традиционного умножения со сдвигом влево включает в себя следующие шаги:

1. Исходное значение суммы частичных произведений принимается равным нулю.

2. Анализируется очередная цифра множителя (анализ начинается со старшей цифры). Если она равна единице, то к СЧП прибавляется множимое, в противном случае (цифра равна нулю) прибавление не производится.

3. Выполняется сдвиг суммы частичных произведений влево на одни разряд.

4. Пункты 2 и 3 последовательно повторяются для всех цифровых разрядов множителя.

На рис. 7.17 приведен пример умножения со сдвигом влево (10 х 11).

Описанная процедура может быть реализована с помощью схемы, показанной на рис. 7.18.

К преимуществу алгоритма сдвига влево следует отнести то, что он позволяет совмещать во времени операции сложения и сдвига. Однако, по сравнению с алгоритмом сдвига вправо, он имеет и ряд недостатков. В первую очередь, СЧП и множитель не могут совместно использовать один и тот же регистр. Для реализации алгоритма требуется 2n-разрядный сумматор. Кроме того, схема со сдвигом влево неудобна при выполнении умножения над числами с разными знаками.

Тем не менее окончательный выбор между алгоритмами сдвига вправо или влево не однозначен. Так, если в результате умножения требуется результат только одинарной длины, то вариант со сдвигом влево может оказаться в аппаратурном плане выгоднее, поскольку не принуждает вводить дополнительные цепи сдвига. Конечный выбор определяется соотношением затрат оборудования на реализацию цепей сдвига и дополнительных разрядов сумматора.

Рис. 7.17. Пример умножения со сдвигом суммы частичных произведений влево

Рис, 7.18. Схема устройства умножения по алгоритму левого сдвига

Умножение чисел со знаком

Несколько сложнее обстоит дело с умножением чисел со знаком, когда n-разрядные сомножители содержат знак (в старшем разряде слова) ия-1 значащую цифру. В дальнейшем условимся отделять знаковый разряд точкой, не забывая, однако, что знаковый разряд участвует в операции наряду с цифровыми разрядами.

Наиболее очевидная мысль — получить абсолютные значения операндов и перемножить их как числа без знака. Справедливость такого решения видна из примера, приведенного на рис. 7.19, где показан процесс умножения чисел +13 и +10.

Во всех ВМ общепринято представлять числа со знаком в форме с фиксированной запятой в дополнительном коде. Положительные числа в этом представлении не отличаются от записи в прямом коде, а отрицательные записываются в виде

Рис. 7.19. Умножение чисел при положительных сомножителях

n -х, где x — фактическое значение числа. В двоичной системе запись отрицат
ельного числа в дополнительном коде сводится к инвертированию всех цифровых разрядов числа, представленного в прямом коде, и прибавлению единицы к младшему разряду получившегося после инвертирования обратного кода. По этой причине более предпочтительны варианты, не требующие преобразования сомножителей и обеспечивающие вычисления непосредственно в дополнительном коде.

Задержимся па особенностях операции умножения при различных сочетаниях знаков сомножителей. Первая из них проявляется при выполнении операции арифметического сдвига вправо для суммы частичных произведений — освободившиеся при сдвиге цифровые позиции должны заполняться не нулем, а значением знакового разряда сдвигаемого числа. Здесь, однако, следует учитывать, что это правило заполнения освободившихся цифровых разрядов начинает действовать лишь с момента, когда среди анализируемых разрядов множителя появляется первая единица.

Множимое произвольного знака,

Пример для положительных сомножителей (А > О, В > 0) уже был рассмотрен.

В случае отрицательного множимого процедура умножения протекает аналогично, с учетом сделанного замечания об арифметическом сдвиге СЧП, что подтверждает пример, приведенный на рис. 7.20.

Поскольку результат умножения отрицательный, он получается в дополнительном коде.

Множимое произвольного знака,

Так как множитель отрицателен, он записывается в дополнительном коде:

[В] д = 2 n – |В|, и в цифровых разрядах кода будет представлено число 2 n -1 -|В|.

При типовом умножении (как и случае В > 0) получим Р = А х (2 n -1 — |В|)=

= -|В|х A+ A х 2 n -1 . Псевдопроизведение Р больше истинного произведения P

Рис. 7.20. Умножение чисел при отрицательном множимом и положительном множителе

на величину А х 2 n -1 , что и необходимо учитывать при формировании окончательного результата. Для этого перед последним сдвигом из полученного псевдопроизведения необходимо вычесть избыточный член. На рис. 7.21 и 7.22 приведены примеры умножения положительного и отрицательного множимого на отрицательный множитель, в которых видна упомянутая коррекция результата.

Рис. 7.21. Умножение чисел при положительном множимом и отрицательном множителе

Рассмотренные процедуры умножения чисел со знаком в принципе могут быть реализованы с помощью ранее рассмотренного устройства (см. рис. 7.16). На практике для перемножения чисел со знаком применяют иные алгоритмы. Наиболее распространенным из них является, алгоритм Бута, имеющий дополнительное преимущество, — он ускоряет процесс умножения по сравнению с рассмотренным ранее. Этот алгоритм будет рассмотрен ниже.

Рис. 7.22. Умножение чисел при отрицательном множимом и отрицательном множителе

У
множение целых чисел и правильных дробей

Рассмотренные алгоритмы относились к представлению чисел с фиксированной запятой, то есть, как это принято в большинстве ВМ, к целым числам, При перемножении чисел со знаком необходимо принимать во внимание, что произведение двух n-разрядных чисел со знаком (знак и n-1 значащий разряд) может иметь 2n-1 значащих разрядов и для его хранения обычно используют регистр двойной длины (2n разрядов). Поскольку число итераций в операции умножения определяется количеством цифровых разрядов множителя, окончательный результат может размещаться в разрядной сетке двойного слова неверно, что и имеет место при перемножении целых чисел (рис. 7.23). Как видно, младший разряд произведения целых чисел, имеющий вес 2°, размещается в позиции двойного слова, соответствующей весу 2 1 . Таким образом, для правильного расположения произведения в разрядной сетке двойного слова необходим дополнительный сдвиг вправо. Такой сдвиг можно учесть как в аппаратуре умножителя, так и программным способом.

С другой стороны, при перемножении правильных дробей дополнительный сдвиг не нужен (см. рис. 7.23). Это обстоятельство необходимо принимать во внимание при построении умножителя для чисел в форме с плавающей запятой, где участвующие в операции мантиссы представлены в нормализованном виде, то есть правильными дробями.

При умножении правильных дробей часто ограничиваются результатом, имеющим одинарную длину. В этом случае может применяться либо отбрасывание лишних разрядов, либо округление.

Ускорение целочисленного умножения

Методы ускорения умножения можно условно разделить на аппаратные и логические. Те и другие требуют дополнительных затрат оборудования, которые при использовании аппаратных методов возрастают с увеличением разрядности сомножителей. Аппаратные способы приводят к усложнению схемы умножителя, но не затрагивают схемы управления. Дополнительные затраты оборудования при реа-лизации логических методов не зависят от разрядности операндов, но схема уп-равления умножителя при этом утяжеляется. На практике ускорение умножения часто достигается комбинацией аппаратных и логических методов.

Логические методы ускорения умножения

Логические подходы к убыстрению умножения можно подразделить на две группы:

— методы, позволяющие уменьшить количество сложений в ходе умножения;

— методы, обеспечивающие обработку нескольких разрядов множителя за шаг.

Реализация и тех и других требует введения дополнительных цепей сдвига в регистры.

Рассмотрим первую группу логических методов.

В основе алгоритма Бута [63] лежит следующее соотношение, характерное для

последовательностей двоичных цифр:

где m и k — номера крайних разрядов в группе из последовательных единиц.

Например, 011110 = 25- 21. Это означает, что при наличии в множителе групп из нескольких единиц (комбинаций вида 011,110), последовательное добавление к СЧП множимого с нарастающим весом (от2 k до 2 m ) можно заменить вычитанием из СЧП множимого с весом 2 k и прибавлением к СЧП множимого с весом 2 m +1 .

Как видно, алгоритм предполагает три операции: сдвиг, сложение и вычитания. Помимо сокращения числа сложений (вычитании) у него есть еще одно достоинство — он в равной степени применим к числам без знака и со знаком.

Алгоритм Бута сводится к перекодированию множителя из системы (О,1) в избыточную систему (-1,0, 1), из-за чего его часто называют перекодированием Бута (Booth recoding). В записи множителя в новой системе 1 означает добавление множимого к сумме частичных произведений, -1 — вычитание множимого u 0 не предполагает никаких действий. Во всех случаях после очередной итерации производится сдвиг множимого влево или суммы частичных произведений вправо. Реализация алгоритма предполагает последовательный в направлении справа налево анализ пар разрядов множителя — текущего Ь i и предшествующего b i -1 , (b i , b i -1 ). Для младшего разряда множителя (i = 0) считается, что предшествующий разряд равен 0, то есть имеет место пара b 0 0..На каждом шаге i (i = 0,1. и — 1) анализируется текущая комбинация b i , b i -1.

Комбинация 10 означает начало цепочки последовательных единиц, и в этом

случае производится вычитание множимого из СЧП.

Комбинация 01 соответствует завершению цепочки единиц, и здесь множимое прибавляется к СЧП.

Комбинация 00 свидетельствует об отсутствии цепочки единиц, а 11 — о нахождении внутри такой цепочки. В обоих случаях никакие арифметические операции не производятся.

По завершении описанных действий осуществляется сдвиг множимого влево либо суммы частичных произведений вправо, и цикл повторяется для следующей пары разрядов множителя.

Описанную процедуру рассмотрим на примерах (используется вариант со сдвигом множимого влево). В приведенных примерах операция вычитания, как это

принято в реальных умножителях, выполняется путем сложения со множителем,

взятым с противоположным знаком и представленным в дополнительном коде.

Напомним, что для удлинения кода до нужного числа разрядов в дополнительные

позиции слева заносится значение знакового разряда.

Пример 1.0110×0011 = 00010010 (в десятичном виде 6×3 = 18). После перекодирования Бута множитель (0, 0,1, 1) приобретает вид (0, 1, 0, -1).

Вначале сумма частичных произведений принимается равной нулю — 00000001).

Полагается, что младшему разряду множителя предшествовал 0. Дальнейший процесс поясняет рис. 7.24.

При наиболее благоприятном сочетании цифр множителя количество суммирований равно n/2, где n — число разрядов множителя.

Модифицированный алгоритм Бута

На практике большее распространение получила модификация алгоритма Бута,

где количество операций сложения при любом сочетании единиц и нулей в множителе всегда равно n/2. В модифицированном алгоритме производится перекодировка цифр множителя из стандартной двоичной системы (0, 1) в избыточную систему (-2. -1, 0, 1, 2), где каждое число представляет собой коэффициент, на который умножается множимое перед добавлением к СЧП. Одновременно анализируются три разряда множителя b i +1 b i b i -1 (два текущих и старший разряд из предыдущей тройки) и, в зависимости от комбинации 0 и 1 в этих разрядах, выполняется прибавление или вычитание множимого, прибавление или вычитание удвоенного множимого, либо никакие действия не производятся (табл. 7.1).

Таблица 7.1. Логика модифицированного алгоритма Бута

Пример вычисления произведения 011001 х 101 ПО = 011000111110 (в десятичном виде 25 х (-18) = -450) показан па рис. 7.26.

Рис. 7.26. Пример умножения (18х (-25)) в соответствии с модифицированным

Еще большее сокращение количества сложений может дать модификация, предложенная Леманом [151]. Здесь, даже при наименее благоприятном сочетании цифр множителя, количество операций сложения не превышает величины n/2, а в среднем же оно составляет n/3. Суть модификации заключается в следующем: — если две группы нулей разделены единицей, стоящей в k -й позиции, то вместо вычитания в k -й позиции и сложения в (к + 1)-й позиции достаточно выполнить только сложение в k -й позиции;

— если две группы единиц разделены нулем, стоящим в k -й позиции, то вместо сложения в k -й позиции и вычитания в (k + 1)-й позиции достаточно выполнить только вычитание в k-й позиции.

Обработка двух разрядов множителя за шаг

Из второй группы логических методов остановимся на умножении с обработкой за шаг двух разрядов множителя (IBM 360/370). В принципе это более эффективная версия алгоритма Бута. Анализ множителя начинается с младших разрядов. В зависимости от входящей двухразрядной комбинации предусматриваются следующие действия:

— 00 — простой сдвиг на два разряда вправо суммы частичных произведений (СЧП);

— 01 — к СЧП прибавляется одинарное множимое, после чего СЧП сдвигается на 2 разряда вправо;

— 10 — к СЧП прибавляется удвоенное множимое, и СЧП сдвигается па 2 разряда вправо;

— 11 — из СЧП вычитается одинарное множимое, и СЧП сдвигается па 2 разряда вправо. Полученный результат должен быть скорректирован на следующей шаге, что фиксируется в специальном триггере признака коррекции. Так как в случае пары 11 из СЧП вычитается одинарное множимое вместо прибавления утроенного, для корректировки результата к СЧП перед выполнением сдвига надо было бы прибавить учетверенное множимое. Но после сдвига на два разряда вправо СЧП уменьшается в четыре раза, так что на следующем шаге достаточно добавить одинарное множимое. Это учитывается при обработке следующей пары разрядов множителя, путем обработки пары 00 как 01, пары 01 как 10, а 10 — как 11, а 11 — как 00. В последних двух случаях фиксируется признак коррекции.

Таблица 7.2. Формирование признака коррекции

Пэра разрядов множителя

+1 из предыдущей пары

+ 1 в следующую пару

Правила обработки пар разрядов множителя с учетом признака коррекции приведены в табл. 7.2. После обработки каждой комбинации содержимое регистра множителя и сумматора частичных произведений сдвигается на 2 разряда вправо. Данный метод умножения требует корректировки результата, если старшая пара разрядов множителя равна 11 или 10 и состояние признака коррекции единичное. В этом случае к полученному произведению должно быть добавлено множимое.

Аппаратные методы ускорения умножения

Традиционный метод умножения за счет сдвигов и сложений, даже при его аппаратной реализации, не позволяет достичь высокой скорости выполнения операции умножения. Связано это, главным образом, с тем, что при добавлении к СЧП очередного частичного произведения перепое должен распространиться от младшего разряда СЧП к старшему. Задержка из-за распространения переноса относительно велика, причем она повторяется при добавлении каждого ЧП.

Одни из способов ускорения умножения состоит в изменении системы кодирования сомножителей, за счет чего можно сократить количество суммируемых частичных произведений. Примером такого подхода может служить алгоритм Бута.

Еще один ресурс повышения производительности умножителя — использование более эффективных способов суммирования ЧП, исключающих затраты времени на распространение переносов. Достигается это за счет представления ЧП в избыточной форме, благодаря чему суммирование двух чисел не связано с распространением переноса вдоль всех разрядов числа. Наиболее употребительной Формой такого избыточного кодирования является так называемая форма сохранением переноса. В ней каждый разряд числа представляется двумя битами cs , известными как перенос (с) и сумма (s). При суммировании двух чисел в форме сохранением переноса перенос распространяется не далее, чем на один разряд.

Это делает процесс суммирования значительно более быстрым, чем в случае сложения с распространением переноса вдоль всех разрядов числа.

Наконец, третья возможность ускорения операции умножения заключу в параллельном вычислении всех частичных произведений. Если paccмотреть общую схему умножения (рис. 7.27), то нетрудно заметить, что отдельные разряды ЧП представляют собой произведения вида a i b j ,то есть произведение определенного бита множимого на определенный бит множителя. Это позволяет вычислить все биты частичных произведений одновременно, с помощью п 2 схем «И». При перемножении чисел в дополнительном коде отдельные разряды ЧП могут иметь вид Тогда элементы «И» заменяются

элементами, реализующими соответствующую логическую функцию.

Рис. 7.27. Схема перемножения n-разрядных чисел без знака

Таким образом, аппаратные методы ускорения умножения сводятся:

— к параллельному вычислению частичных произведений;

— к сокращению количества операций сложения;

— к уменьшению времени распространения переносов при суммировании частичных произведений.

Все три подхода в любом их сочетании обычно реализуются с помощью комбинационных устройств.

Параллельное вычисление ЧП имеет место практически во всех рассматриваемых ниже схемах умножения. Различия проявляются в основном в способе суммирования полученных частичных произведении, и с этих позиций используемые схемы умножения можно подразделить на матричные и с древовидной структурой. В обоих вариантах суммирование осуществляется с помощью массива взаимосвязанных одноразрядных сумматоров. В матричных умножителях сумматоры организованы в виде матрицы, а в древовидных они реализуются в виде дерева того или много типа.

Различия в рамках каждой из этих групп выражаются в количестве используемых сумматоров, их виде и способе распространения переносов, возникающих в процессе суммирования.

В матричных умножителях суммирование осуществляется матрицей сумматоров, состоящей из последовательных линеек (строк) одноразрядных сумматоров с сохранением переноса (ССП). По мере движения данных вниз по массиву сумматоров каждая строка ССП добавляет к СЧП очередное частичное произведение. Поскольку промежуточные СЧП представлены в избыточном форме с сохранением переноса, во всех схемах, вплоть до последней строки, где формируется окончательный результат, распространения переноса не происходит. Это означает, что задержка в умножителях отталкивается только от «глубины» массива (числа строк сумматоров) и не зависит от разрядности операндов, если только в последней строке матрицы, где формируется окончательная СЧП, не используется схема с последовательным переносом.

Наряду с высоким быстродействием важным достоинством матричных умножителей является их регулярность, что особенно существенно при реализации таких умножителей в виде интегральной микросхемы. С другой стороны, подобные ‘схемы занимают большую площадь на кристалле микросхемы, причем с увеличением разрядности сомножителей эта площадь увеличивается пропорционально квадрату числа разрядов. Вторая проблема с матричными умножителями — низкий уровень утилизации аппаратуры. По мере движения СЧП вниз каждая строка задействуется лишь однократно, когда со пересекает активны и фронт вычислений. Это обстоятельство, однако, может быть затребовано для повышения эффективности вычислений путем конвейеризации процесса умножения, при которой по мере освобождения строки сумматоров последняя может быть использована для умножения очередной пары чисел.

Ниже рассматриваются различные алгоритмы умножения и соответствующие им схемы матричных умножителей. Каждый из алгоритмов имеет своп плюсы и минусы, важность которых для пользователя определяет выбор той или иной схемы.

Матричное умножение чисел без знака

Результат Р перемножения двух n-разрядных двоичных целых чисел А и В без знака можно описать выражением

Умножение сводится к параллельному формированию битов из п n-разрядных частичных произведений с последующим их суммированием с помощью матрицы сумматоров, структура которой соответствует приведенной матрице умножения. Схема известна как умножитель Брауна. На рис. 7.28 показан такой умножитель для четырехразрядных двоичных чисел, в котором каждому столбцу в матрице умножения соответствует диагональ умножителя. Биты частичных произведений (ЧП) вида a i b j формируются с помощью элементов «И». Для суммирования ЧП Применяются два вида одноразрядных сумматоров с сохранением переноса: полусумматоры (ПС) 1 и полные сумматоры (СМ).

1 Полусумматоры называется одноразрядное суммирующее устройство, имеющее дна входа для слагаемыx и два входа и два выхода — выход бита суммы и выход бита переноса.

Рис. 7.28. Матричный умножитель Брауна для четырехразрядных чисел без знака

Матричный умножитель п х п содержит п г схем «И», ПС и (п 2 — 2п) СМ.Если принять, что для реализации полусумматора требуются два логических элемента, а для полного сумматора — пять, то общее количество логических элементов в умножителе составляет п 2 + 2п + 5(п 2 — 2л) = 6п 2 – 8n.

Быстродействие умножителя определяется наиболее глинным маршрутом распространения сигнала, который в худшем случае (пунктирная линия на рис. 7.28) включает в себя прохождение одной схемы «И», двух ПС и (2п — 4) СМ. Полагая задержки в схеме «И» и полусумматоре равными Л, а в полном сумматоре — 2Д. общую задержку в умножителе можно оценить выражением <4 n - 5)Д. Чтобы сократить ее длительность, n-разрядный сумматор с последовательным переносом в нижней строке умножителя можно заменить более быстрым вариантом сумматора. Последнее, однако, не всегда желательно, поскольку это увеличивает число используемых в умножителе логических элементов и ухудшает регулярность схемы.

В общем случае задержка в матричных умножителях пропорциональна их разрядности: 0(п).

Матричное умножение чисел в дополнительном коде

К сожалению, умножитель Брауна годится только для перемножения чисел знака. При обработке знаковых чисел отрицательные представляются дополнительным кодом, а матричные умножителя строятся по схемам, отличным от схемы Брауна. Прежде всего, напомним, что запись двоичного тела в дополнительном коде (с дополнением до 2) имеет вид ‘£»

член правого выражения представляет знак числа, а сумма — его модуь.

Исходя из приведенной записи, произведение Р двух n-разрядных двоичных целых чисел А и В в дополнительном коде (значение произведения и сомножителей в дополнительном коде обозначим соответственно V ( P ), V < A ) и V ( B )) можно

Матрица умножения чисел со знаком, представленных в дополнительном коде, похожа на матрицу перемножения чисел без знаков (рис. 7.29). Отличие состоит в том, что (2n — 2) частичных произведений инвертированы, а в столбцы п и (2n — 1) добавлены единицы.

Рис. 7.29. Матрица перемножения n-разрядных чисел а дополнительном кода

Соответствующая схема матричного умножителя для четырёхразрядных чисел показана на рис. 7.30.

Здесь (2n — 2) частичных произведений инвертированы за счет замены элемента «И» на элементы «И-НЕ». Сумматор в младшем разряде нижнего ряда складывает 1 в столбце n с вектором сумм и переносов из предшествующей строки, реализуя при этом следующие выражения:

Инвертор в нижней строке слева обеспечивает добавление единицы, в столбец (2n-1).

Рис. 7.30. Матричный умножитель для четырехразрядных чисел в дополнительном коде

Несколько иная схема матричного умножителя, также обеспечивающего умножение чисел в дополнительном коде, была предложена Бо и Були [61]. В алгоритме Бо-Вули произведение чисел в дополнительном коде представляется следующим соотношением:

Матрица умножения, реализующая алгоритм, приведена на рис. 7.31, а соответствующая ей схема умножителя — на рис. 7.32. . ‘

По ходу умножения частичные произведения, имеющие знак «минус», смещаются к последней ступени суммирования. Недостатком схемы можно считать то, что на последних этапах работы требуются дополнительные сумматоры, из-за чего регулярность схемы нарушается.

Рис. 7.31. Матрица перемножения n-разрядных чисел согласно алгоритму Бо-Вули

Рис. 7.32. Матричный умножитель для четырехразрядных чисел в дополнительном коде по схеме Бо-Вули

Еще один алгоритм для вычисления произведения чисел в дополнительном коде был предложен Пезарисом [181].

При представлении числа в дополнительном коде старший разряд числа имеет отрицательный вес. Для учета этого обстоятельства Пезарис выдвигает идею использовать в умножителе четыре вида полных сумматоров (рис. 7.33).

Рис. 7.33. Виды сумматоров, применяемых в матричном умножителе Пезариса

В сумматоре типа СМО, который фактически является обычным полным сумматором. все входные данные (x, у, z ) имеют положительный вес, а результат лежит в диапазоне 0-3. Этот результат представлен двухразрядным двоичным числом cs , где с и s также присвоены положительные веса. В остальных трех типах сумматоров некоторые из сигналов имеют отрицательный вес. Схема умножений в рассматриваемом методе показана на рис. 7.34.

Рис. 7-34. Матрица перемножения n-разрядных чисел согласно алгоритму Пезариса

Здесь знак «минус» трактуется следующим образом: -1 = -2 * 1 + 1; -0 = -2 * 0 + 0. Схема умножителя, реализующего алгоритм Пезариса, приведена на рис. 7.35.

По сравнению с умножителем Бо-Вули, схема Пезариса имеет более регулярный вид, но, с другой стороны, она предполагает присутствие нескольких типов сумматоров.

Сократить задержку, свойственную матричным умножителям, удается в схемах, построенных по древовидной структуре. Если в матричных умножителях для cсуммирования п частичных произведений требуется п строк сумматоров, то в древовидных схемах количество ступеней сумматоров пропорционально Iog 2 n (рис. 7.3(3)-Соответственно числу ступеней суммирования сокращается и время вычисления СЧП. Хотя древовидные схемы быстрее матричных, однако при их реализации требуются дополнительные связи для объединения разрядов, имеющих одинаковый вес, из-за чего площадь, занимаемая схемой на кристалле микросхемы, может оказаться даже больше, чем в случае матричной организации сумматоров. Еще одна проблема связана с тем, что стандартное двоичное дерево не является самой эффективной древовидной иерархией, поскольку не позволяет в полной мере

Рис. 7.35. Матричный умножитель для четырехразрядных чисел в дополнительном коде по схеме Пезариса

Рис. 7.36. Суммирование частичных произведений в умножителях: а — с матричной структурой; б — со структурой двоичного дерева

воспользоваться возможностями полного сумматора (имеющего не два, а три входа), благодаря чему можно одновременно суммировать сразу три входных бита. По этой причине на практике в умножителях с древовидной структурой применяет иные древовидные схемы. С другой стороны, такие схемы не столь регулярны, как двоичное дерево, а регулярность структуры — одно из основных требований при создании интегральных микросхем.

Древовидные умножители включают в себя три ступени:

— ступень формирования битов частичных произведений, состоящую из п 2 элементов «И»;

— ступень сжатия частичных произведений — реализуется в виде дерева параллельных сумматоров (накопителей), служащего для сведения частичных произведений к вектору сумм и вектору переносов. Сжатие реализуется несколькими рядами сумматоров, причем каждый ряд вносит задержку, свойственна одному полному сумматору;

— ступень заключительного суммирования, где осуществляется сложение вектора сумм и вектора переносов с целью получения конечного результата. Обычно здесь применяется быстрый сумматор с временем задержки, пропорциональным O ( log 2 ( n )).

Известные древовидные умножители различаются по способу сокращения числа ЧП. При использовании в умножителе СМ и ПС их обычно называют счетчиками (3,2) и (2,2) соответственно. Связано это с тем, что код на выходах стал, как и в двоичном счетчике, равен количеству единиц, поданных на входы.

Процесс «компрессии» СЧП завершается формированием двух векторов — вектора сумм и вектора переносов, которые для получения окончательного результата обрабатываются многоразрядными сумматорами, то есть различие между древовидными схемами сжатия касается, главным образом, способа формирования упомянутых векторов.

В известных на сегодня умножителях наибольшее распространение получили три древовидных схемы суммирования ЧП: дерево Уоллеса, дерево Дадда и перевернутое ступенчатое дерево. В наиболее общей формулировке дерево Уоллеса — это оператор с п входами и log 2 n выходами, в котором код на выходе равен числу единиц во входном коде. Вес битов на входе совпадает с весом младшего разряда выходного кода. Простейшим деревом Уоллеса является СМ. Используя такие сумматоры, а также полусумматоры, можно построить дерево Уоллеса для перемножения чисел любой разрядности, при этом количество сумматоров возрастает пропорционально величине \ og 2 n . В такой же пропорции растет время выполнения операции умножения,. Согласно алгоритму Уоллеса, строки матрицы частичных произведений группируются по три. Полные сумматоры используются для сжатия столбцов с тремя битами, а полусумматоры — столбцов с двумя битами. Строки, не попавшие в набор из трех строк, учитываются в следующем каскаде редукции. Количество строк в матрице (ее высота) на j-й ступени определяется выражениями

В 32-разрядном умножителе на базе дерева Уоллеса высоты матриц ЧП последовательно уменьшаются в последовательности: 22, 15, 10, 7, 5, 4, 3 и 2. Логика построения дерева Уоллеса для суммирования частичных произведений в умножителе 4×4 показана на рис. 7.37, а. Для пояснения структуры дерева сумматоров часто применяют так называемую точечную диаграмму (рис. 7.37, 6). В ней точки обозначают биты частичных произведений, прямые диагональные линии представляют выходы полных сумматоров, а перечеркнутые диагонали — выходы полусумматоров. Хотя на рис. 7.37, а в третьем каскаде показаны три строки, фактически после редукции остаются лишь две первых, а третья лишь отражает переносы, которые учитываются при окончательном суммировании. Этим объясняется кажущиеся отличие от точечной диаграммы.

Рис. 7.37. Суммирование ЧП с помощью дерева Уоллеса (вариант 1): а — логика суммирования; б — точечная диаграмма

Умножитель (рис. 7.38) состоит из трех ступеней с высотами 4,3,2 и содержит 16 схем «И», 3 полусумматора, 5 полных сумматоров. Сложение векторов сумм и переносов в последнем каскаде реализуется четырехразрядным сумматором с последовательным распространением переноса, однако чаще для ускорения привлекаются более эффективные схемы распространения переноса, например параллельная. Отметим, что избыточность кодирования, заложенная в алгоритм Уоллеса, приводит к тому, что возможно построение различных вариантов схемы дерева. Так, LpHc. 7.39 показана иная реализация дерева Уоллеса для четырехразрядных операндов. Как видно, новый вариант схемы никакого выигрыша в аппаратурном плане не дает.

Схема Уоллеса считается наиболее быстрой, но в то же время ее структура наименее регулярна, из-за чего предпочтение отдается иным древовидным структурам. Основная сфера использования умножителей со схемой Уоллеса — перемножение чисел большой разрядности. В этом случае быстродействие имеет превалирующее значение.

При умножении чисел небольшой разрядности более распространена другая схема сжатия суммирования ЧП — схема дерева Л. Дадда. В ее основе также лежит дерево Уоллеса, но реализуемое минимальным числом сумматоров.

Рис. 7.38. Умножитель 4×4 со структурой дерева Уоллеса

Рис. 7,39. Суммирование ЧП с помощью дерева Уоллеса (вариант 2): а — логика суммирования; б — точечная диаграмма

Схема редукции, предложенная Л. Даддом, начинается с определения высоты промежуточных матриц частичных произведений: , пока dj Значения для dj приведены в табл. 7.3.

Так, 32-разрядный умножитель на базе дерева Дадда имеет высоты промежуточных матриц 29,19,13,9,6,4,3 и 2. На j-й от конца ступени умножителя используетcя минимальное число ПС и СМ, позволяющее сократить число битов в столбце d j . Если высота столбца, включающая переносы, равна h , то число полусумматоров (N nc ) и полных сумматоров

(N СМ ) составляет:

На рис. 7.40 описан умножитель 4 х 4, реализующий алгоритм дерева Дадда. Для этого требуется 16 схем «И», два полусумматора, четыре полных сумматора и шестиразрядный сумматор. Схема содержит три ступени с высотами промежуточных матриц: 4,3 и 2. На этапе суммирования вектора сумм и вектора переносов необходим (2п — 2)-разрядный сумматор.

рис. 7.40. Суммирование ЧП с помощью дерева Дадда для случая чисел без знака: а — логика суммирования; б — точечная диаграмма

Схема умножения чисел в дополнительном коде, рассмотренная применительно к матричному умножителю, может быть адаптирована и для умножителя со схемой Дадда. В таком случае схема сжатия приобретает вид, показаний на рис. 7.41.

Рис. 7.41. Суммирование ЧП в дополнительном коде с помощью дерева Дадца: а — логика суммирования; б — точечная диаграмма

Различия методов Уоллеса и Дадда являются следствием разных подходов к решению задачи «компрессии» суммирования. Алгоритм Уоллеса ориентированы на сжатие кодов как можно раньше, на самых ранних этапах, а алгоритм Дадда стремится это сделать по возможности позже, то есть наибольший уровень сжатия относит к завершающим стадиям.

Сравнивая схемы Уоллеса и Дадда, можно отмстить, что число каскадов сжатия в них одинаково, однако количество используемых полусумматоров и полных сумматоров в схеме Дадда меньше (при подсчете числа элементов обычно не учитывают многоразрядные сумматоры, предназначенные для окончательного сложения векторов сумм и переносов). С другой стороны, на этапе сложения векторов сумм и переносов в варианте Уоллеса требуется сумматор с меньшим числом разрядов (в нашем примере — 4 против 6).

У обеих схем имеется общий недостаток — нерегулярность структуры, особенно у дерева Уоллеса.

Схема перевернутой лестницы (overturned stairs), предложенная в [169], являет собой одну из попыток сделать древообразную структуру более регулярной, а значит, облегчить ее реализацию в интегральном исполнении. «Лестница* строится из базовых блоков трех видов (рис. 7.42, я), которые авторы назвали «ветвью» (branch), «соединителем» (connector) и «корнем» (root).

Базовые элементы объединяются, образуя дерево, имеющее п входов. Подобная схема на 18 входов показана на рис. 7.42,6. Как видно, дерево имеет достаточно

Рис. 7.42. Перевернутое дерево: а — базовые блоки; б — структура дерева на 18 входов

регулярную структуру, однако нужно учитывать, что веса отдельных входов различаются. Кроме того, конструкция умножителя получается сложной.

Сравнительная оценка схем умножения с матричной и древообразной структурой

В табл. 7.4 приведены данные по производительности различных видов умножителей, выполненных средствами интегральной схемотехники. Быстродействие умножителей характеризуется коэффициентом при величине задержки l в одном Логическом элементе.

Таблица 7.4. Сравнение производительности умножителей в интегральном исполнении

Содержимое таблицы плюс некоторые не включенные в нее данные позволяет сделать следующие выводы. Наиболее быстро работают умножители, построенные по схеме Бута, а также имеющие древовидную структуру, в частности дерево Дадда. Для операндов длиной в 16 разрядов и более наиболее привлекательной представляется модифицированная схема Бута, как по скорости, так и по затратам оборудования. Максимально быстрое выполнение операции умножения обеспечивает сочетание алгоритма Бута и дерева Уоллеса. С другой стороны, достаточно хорошие показатели скорости при умножении чисел небольшой разрядности выдает схема Бо-Вули. В плане потребляемой мощности наиболее экономичными являются умножители, построенные по схемам Брауна и Пезариса. Несмотря на сравнительно небольшое число используемых транзисторов, схемы на базе алгоритма Бута, а также древовидные реализации, потребляют больше из-за избыточных внутренних связей, связанных с нерегулярной структурой этих схем.

Конвейеризация параллельных умножителей

В матричной и древовидной структурах параллельных умножителей заложен еще один потенциал повышения производительности — возможность конвейеризации. При конвейеризации весь процесс вычислений разбивается на последовательность законченных шагов. Каждый из этапов процедуры умножения выполняется на своей ступени конвейера, причем все ступени работают параллельно. Результаты, полученные на i -ой ступени, передаются на дальнейшую обработку в (i + 1)-ю ступень конвейера. Перенос информации со ступени на ступень происходит через буферную память, размещаемую между ними (рис. 7.43).

Рис. 7.43. Структура конвейерного умножителя

Выполнившая свою операцию ступень помещает результат в буферную нам и может приступать к обработке следующей порции данных операций, в то время как очередная ступень конвейера в качестве исходных использует данные, хранящиеся в буферной памяти на ее входе. Синхронность работы конвейера обеспечивается тактовыми импульсами, период которых определяется самой медленной ступенью конвейера и задержкой в элементе буферной памяти …Несмотря на то что время выполнения операции умножения для каждой конкретной пары сомножителей в конвейерном умножителе не только не уменьшается, но даже несколько увеличивается за счет задержек в буферной памяти при последовательном перемножении последовательностей пар сомножителей, достигаемый выигрыш весьма ощутим. Действительно, в конвейерном умножителе из k ступеней перемножаемые данные могут подаваться на вход с интервалом в k раз меньшим, чем в случае обычного умножителя. В том же темпе появляются и результаты на выходе,

Схема конвейера легко может быть применена к матричным и древовидным умножителям. В матричных умножителях в качестве ступени конвейера выступает каждая строка матрицы сумматоров. В качестве примера конвейеризированного матричного умножителя на рис. 7.44 приведена схема 4×4. Черными прямоугольниками обозначены триггеры-защелки, образующие буферную память.

Рис. 7.44. Конвейеризированный матричный умножитель

Конвейеризация матричных умножителей на уровне строк сумматоров может быть затруднительной из-за большого числа ступеней и необходимости введения в состав умножителя значительного количества триггеров-защелок. Сокращение числа триггеров достигается за счет следующих приемов;

— отказа от использования идеи конвейеризации между входными схемами «И» и первой строкой полных сумматоров;

— увеличением времени обработки на каждой ступени, например можно принять его равным удвоенному времени срабатывания полного сумматора;

— отказом от формирования всех п 2 битов частичных произведений в самом начале, перед первой ступенью конвейера, и вычислением их по мере необходимости стало на разных ступенях конвейера.

В древовидных умножителях в качестве ступеней конвейера выступают каскады сжатия, то есть более крупные образования, чем в матричных умножителях. Кроме того, количество каскадов компрессии также значительно меньше. Это делает конвейеризацию древовидных умножителей более привлекательной. На рис. 7.45 показана точечная диаграмма конвейеризированного умножителя со схемой Дадда.

Рис. 7.45. Древовидный конвейеризированный умножитель со схемой Дадда

В правой части рисунка указано количество триггеров-защелок, необходимых каждой ступени конвейера. Как видно, в умножителе Дадда 8×8 требуются 243 триггера, не считая дополнительных триггеров для конвейеризации последнего этапа сложения частичных произведений. Количество триггеров может быть сокращено за счет увеличения времени, выделяемого на выполнение операций ступени конвейера. Это позволяет убрать некоторые из триггеров.

При конвейеризации умножителя на базе дерева Уоллеса требуется меньше триггеров-защелок, поскольку в этой схеме основное сжатие суммы частичных произведений происходит на более ранних этапах. Кроме того, для заключительного суммирования векторов сумм и переносов используется более «короткий» сумматор.

Рекурсивная декомпозиция операции умножения

Как правило, аппаратные умножители, построенные на рассмотренных принципах, имеют ограничение на число разрядов вводимых чисел. Умножитель повышенной разрядности можно получить из модулей меньшей разрядности, выстраивая так называемую рекурсивную декомпозицию операции умножения. Так, для построения умножителя 8×8 можно использовать четыре модуля типа 4 х 4. Множимое А разбивается на четыре старших (А h ) и четыре младших (A l ) разряда. Множитель В таким же образом разбивается на части Четыре модуля типа 4×4 вычисляют соответственно произведения На выходах модулей получаются восьмиразрядные результаты, которые соответствуют частичным произведениям в разрядах: 15-8,11-4, снова 11-4 и 7-0. Окончательный результат формируется путем суммирования этих четырех частичных произведений с учетом их положения в разрядной сетке (рис. 7.46).

Рис. 7.46. Декомпозиция операции умножения

Деление несколько более сложная операция, чем умножение, по базируется на тех же принципах. Основу составляет общепринятый способ деления с помощью операций вычитания или сложения и сдвига (рис. 7.47).

Рис. 7.47. Общая схема операции деления

Задача сводится к вычислению частного Q и остатка S :

Деление выражается как последовательность вычитаний делителя сначала из делимого, а затем из образующихся в процессе деления частичных остатков (Ч0), Делимое обычно представляется двойным словом (2n разрядов), делитель , частное и остаток имеют разрядность п.

Операция выполняется за п итераций и может быть описана следующим образом:

После п итераций получается

Частное от деления 2n-разрядного числа на n-разрядное может содержать более, чем п разрядов. В этом случае возникает переполнение, из-за чего перед выполнением деления необходима проверка условия

Из выражения следует, что переполнения не будет, если число, содержащееся в старших п разрядах делимого, меньше делителя.

Помимо этого требования, перед началом операции необходимо исключите возможность ситуации деления на 0.

Реализовать деление можно двумя основными способами:

— с неподвижным делимым и. сдвигаемым вправо делителем;

— с неподвижным делителем и сдвигаемым влево делимым.

Недостатком первого способа является потребность иметь в устройстве деления сумматор и регистр двойной длины. Второй способ позволяет строить делитель с сумматором одинарной длины. Неподвижный делитель D хранится в регистре с одинарной длины, а делимое Z, сдвигаемое относительно D находится в двух таких же регистрах. Образующиеся цифры частного Q заносятся в освобождаются при сдвиге Z разряды одного из регистров Z .

Ниже на примере чисел без знака рассматриваются два основных алгоритма целочисленного деления.

Деление с восстановлением остатка

Наиболее очевидный алгоритм носит название алгоритма деления с неподвижным делителем и восстановлением остатка. В учебнике он представлен в силу того, что очень похож на общепринятый способ деления столбиком. Данный алгоритм может быть описан следующим образом:

1. Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2. Частичный остаток удваивается путем сдвига па один разряд влево. При этом в освобождающийся при сдвиге младший разряд 40 заносится очередная цифра, частного.

3. Из сдвинутого 40 вычитается делитель и анализируется знак результата вычитания.

4. Очередная цифра модуля частного равна единице, когда результат вычитания положителен, и пулю, если отрицателен. В последнем случае значение остатка восстанавливается до того значения, которое было до вычитания.

5. Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного.

На рис. 7.48 показан процесс деления с восстановлением остатка, здесь число 41 делится на 8.

Деление без восстановления остатка

Недостаток затронутого алгоритма заключается в необходимости выполнения на отдельных шагах дополнительных операции сложения для восстановления частичного остатка. Это увеличивает время выполнения деления, которое в этом случае может меняться в зависимости от конкретного сочетания кодов операндов.

В силу указанных причин реальные делители строятся на основе алгоритм а. деления с неподвижным делителем без восстановления остатка. Приведем описание этого алгоритма.

1. Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2. Частичный остаток удваивается путем сдвига на один разряд влево. При этом в освобождающийся при сдвиге младший разряд 40 заносится очередная цифра частного.

3. Из сдвинутого частичного остатка вычитается делитель, если остаток положителен, и к сдвинутому частичному остатку прибавляется делитель, если остаток отрицательный.

Рис. 7.48. Пример деления с восстановлением остатка

4. Очередная цифра модуля частного равна единице, когда результат вычитаний 1 положителен, и нулю, если он отрицателен. I

5. Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного. Как видим, пункты 1,2,5 полностью совпадают с соответствующими пунктами предыдущего алгоритма деления.

Процесс деления без восстановления остатка для ранее рассмотренного примера демонстрируется на рис. 7.49.

Деление чисел со знаком

Как и в случае умножения, деление чисел со знаком может быть выполнено путем перехода к абсолютным значениям делимого и делителя, с последующим присвоением частному знака «плюс» при совпадающих знаках делимого и делителя либо «минус» — в противном случае.

Деление чисел, представленных в дополнительном коде, можно осуществлять не переходя к модулям. Рассмотрим необходимые для этого изменения в алгоритме без восстановления остатка.

Так как делимое и делитель не обязательно имеют одинаковые знаки, то действия с частичным остатком (прибавление или вычитание D ) зависят от знаков остатка и делителя и определяются содержимым табл. 7.5:

Рис. 7.49. Пример деления без восстановления остатка

Таблица 7.5. Операция, выполняемая в очередной итерации деления

— Если знак остатка совпадает со знаком делителя, то очередная цифра частного — 1, иначе — 0.

— Если Z> 0 и D D > 0, то при ненулевом остатке от деления частное нужно увеличить па единицу.

— Если Z 0 и D Устройство деления

Рассмотренный алгоритм деления без восстановления остатка может быть реализован с помощью устройства, схема которого приведена на рис. 7.50.

Процедура начинается с занесения делимого и 2n-разрядный регистр делимого (РДМ) и делителя n -разрядный регистр делителя (РДТ). В счетчик цикла (СЧЦ — на схеме по покатам), служащий для подсчета количества полученных цифр частного, помещается исходное значение, равное п.

Рис. 7.50. Схема деления по алгоритму без восстановления остатка

На каждом шаге содержимое регистра делимого (РДМ) и регистра частного (РЧ) сдвигается на один разряд влево. В зависимости от сочетания знаков частичного остатка и делителя определяется значение очередной цифры частного и требуемое действие: вычитание пли прибавление делителя. Вычитание делителя производится посредством прибавления дополнительного кода делителя. Преобразование в дополнительный код осуществляется за счет передачи делителя на вход сумматора обратным (инверсным) кодом с последующим добавлением единицы к младшему разряду сумматора.

Описанная процедура повторяется до исчерпания всех цифр делимого, о чем свидетельствует нулевое содержимое счетчика циклов (содержимое СЧЦ уменьшается на единицу после каждой итерации). По окончании операции деления частное располагается в регистре частного, а в регистре делимого будет остаток от деления.

На заключительном этапе, если это необходимо, производится корректировка полученного результата, как это предусматривает алгоритм деления чисел со знаком.

На практике для накопления и хранения частного вместо отдельного регистра используют освобождающиеся в процессе сдвигов младшие разряды регистра делимого.

Комбинированное устройство умножения/деления

Сходство процедур умножения и деления находит свое отражение в близости структур соответствующих устройств (рис. 7.51).

Из подобия процедур вытекает очевидная идея реализации обеих операций с помощью единых технических средств, в виде комбинированного устройства умножения-деления (рис. 7.52).

Рис. 7.51. Структура устройств умножения и деления

Рис. 7.52. Комбинированное устройство умножения/деления

Видим, что для храпения операндов и результатов используются общие регистры. Усложнение связано, главным образом, с устройством управления, функции второго существенно расширяются, что, естественно, требует определенного увеличения аппаратурных затрат.

Ускорение целочисленного деления

Следует отметить, что операция деления предоставляет не слишком много путей для своей оптимизации по времени. Тем не менее определенные возможности для убыстрения деления существуют, и их можно свести к следующим:

— замена делителя обратной величиной, с последующим ее умножением на делимое

— сокращение времени вычисления частичных остатков в традиционных методах деления (с восстановлением или без восстановления остатка) за счет ускорения операций суммирования (вычитания);

— сокращение времени вычисления за счет уменьшения количества операций суммирования (вычитания) при расчете Ч0;

— вычисление частного в избыточной системе счисления.

За исключением первого из перечисленных подходов все прочие фактически являются модификациями традиционного способа деления.

Замена деления умножением на обратную величину

В предыдущем разделе было показано, что операцию умножения можно производить сравнительно быстро, если взять на вооружение комбинационные схемы параллельного умножения. Данное обстоятельство можно использовать, заменив операцию деления на D умножением на

В этом случае проблема сводится к эффективному вычислению X / D . Обычно задача решается одним из двух методов; с помощью ряда Тейлора или метода Ньютона-Рафсона. В обоих случаях основное время расходуется на умножение, поэтому рассматриваемый метод ускорения деления имеет смысл при наличии быстрых схем умножения.

При реализации первого метода делитель D представляется в виде: D = 1+Х. Тогда для двоичного представления D можно записать:

Метод был использован в модели 91 вычислительной машины IBM 360 для вычисления 32-разрядной величины 1/ D . Возможные значения сомножителей в правой части выражения извлекались из таблицы емкостью 28 байт, хранящейся в памяти. Операция вычисления 1/ D требует шести умножений.

Вычисление величины 1/ D методом Ньютона-Рафсона сводится к нахождению корня уравнения

то есть Х= 1 /O. Решение может быть получено с привлечением рекуррентного соотношения: X i + l = X i (2 – X i D ). Количество итераций определяется требуемой точностью вычисления X / D . Реализация метода для n-разрядных чисел требует 2 int(log 2 n) — 1 операций умножения.

В общем, замена операции деления на умножение более характерна для чисел с плавающей запятой.

Ускорение вычисления частичных остатков

Возможности данного подхода весьма ограничены и связаны в основном с ускорением операций сложения (вычитания). Способы достижения этой цели ничем не отличаются от тех, что применяются, например, при выполнении умножения. Это различные приемы для убыстрения распространения переноса, матричные схемы сложения и т. п. В частности, для вычисления частичных остатков может быть применена матричная схема, показанная на рис. 7.53.

Рис. 7.53. Матричное устройство деления для алгоритма без восстановления остатка

Представленная схема реализует алгоритм деления без восстановления остатка для правильных дробей, что типично в операциях над мантиссами чисел в форме с плавающей запятой. Нетрудно заметить, что схеме присущ длинный тракт распространения переноса, что явно не способствует сокращению времени деления. Таким образом, матричное исполнение деления нельзя считать очень эффективным в плане быстродействия, хотя данный метод и выигрывает в сравнении с традиционным устройством деления. Основное достоинство матричной схемы заключается в ее регулярности, что удобно при реализации устройства в виде интегральной микросхемы.

В основе третьей группы методов ускорения операции деления, согласно приведенной выше классификации, лежит так называемый алгоритм SRT [77,184,214]. Свое название алгоритм получил по фамилиям авторов (Sweeney, Robertson, Tocher), разработавших его независимо друг от друга приблизительно в одно и то же время. Этот алгоритм представляет собой модификацию деления без восстановления остатка. В стандартной процедуре па каждом шаге помимо сдвига частичного остатка производится прибавление либо вычитание делителя. В SRT-алгоритме сдвиг Ч0 также имеется в каждой итерации, однако сложение или вычитание в зависимости от получающегося Ч0, на отдельных шагах может не выполняться, что, естественно, позитивно влияет па быстродействие деления.

Алгоритм был ориентирован на операции над мантиссами чисел с плавающей запятой и опирается на то обстоятельство, что мантиссы в таких числах нормализованы. Впервые SRT-алгоритм был реализован и модели 91 вычислительной машины IBM 360. В настоящее время он широко применяется в блоках обработки чисел с плавающей запятой, в частности в микропроцессорах фирмы Intel.

Сначала рассмотрим алгоритм применительно к положительным целым числам. Делимое представляется (2п + 1)-разрядным числом, а делитель — n-разрядным. Процедура деления начинается с удаления в делителе всех нулей, предшествующих старшей единице, то есть с операции, аналогичной нормализации мантиссы в числах с плавающей запятой. По той же аналогии будем в дальнейшем условно называть эту операцию нормализацией. Исключение k предшествующих нулей реализуется за счет сдвига делителя влево на k разрядов. На аналогичное число разрядов влево сдвигается и делимое. Далее выполняются п итерации, в которых вычисляются цифры частного и частичные остатки. Действия, выполняемые на i -й итерации, можно описать следующим образом:

Обратим внимание па то, что частное представляется в системе счисления, отличной от двоичной. Это означает, что цифры частного могут иметь больше, чем. два значения О и 1. В рассматриваемом случае — -1,0, 1.

По завершении всех п итераций, если последний остаток отрицателен, выполняется коррекция этого остатка и полученного частного, для чего к остатку прибавляется делитель, а из частного вычитается единица с весом младшего разряда.

Последний момент в алгоритме — преобразование частного из системы <-1,0,1>в систему <0, 1>, то есть в обычную двоичную систему.

На практике это выливается в следующую процедуру (при объяснении будем ссылаться на схему деления без восстановления остатка, приведенную на рис: 7.50). Делимое и делитель, представленные в дополнительном коде, размещаются в регистре делимого (РДМ) и делителя (РДТ) соответственно. Дальнейшие действия можно описать следующим образом.

1. Если в делителе D имеются к предшествующих нулей (при D > 0) или предшетвующих единиц (при D 0), то производится предварительный сдвиг содержимого РДМ и РДТ влево на k разрядов.

2. Для i от 0 до п — 1:

— если три старших цифры частичного остатка в РДМ совпадают, то q i = О и производится сдвиг содержимого РДМ па один разряд влево;

— если три старших цифры частичного остатка в РДМ не совпадают, а сам ЧО отрицателен, то q i = -1, делается сдвиг содержимого РДМ на один разряд влево и к ЧО прибавляется делитель;

— если три старших цифры частичного остатка в РДМ не совпадают, а сам ЧО положителен, то q i = 1, выполняется сдвиг содержимого РДМ на разряд влево и из ЧО вычитается делитель.

3. Если после завершения пункта 2 остаток отрицателен, то производится коррекция (к остатку прибавляется делитель, а из частного вычитается единица).

4. Остаток сдвигается вправо на k разрядов.

Описанную процедуру иллюстрирует пример, приведенный на рис. 7.54.

Рис. 7.54. Пример деления целых чисел по алгоритму SRT

На первом шаге для удаления предшествующих нулей делитель сдвигается на два разряда влево. Аналогично поступают и с ЧО, который вначале совпадает с делимым. Далее выполняется процедура, описанная выше в пункте 2. Операция вычитания D обеспечивается прибавлением делителя с противоположным знаком. Поскольку по завершении операции остаток отрицателен, производится его коррекция путем прибавления D . Одновременно частное уменьшается на единицу (эта операция показана в системе <-1,0, 1>, в которой представлено частное). Наконец, на последнем шаге форма представления частного меняется, переходят к представлению в стандартной двоичной системе.

В стандартном алгоритме деления без восстановления остатка помимо сдвига в каждой итерации выполняется операция сложения или вычитания. В варианте SRT, в зависимости от кодов операндов в отдельных итерациях, достаточно только сдвига, что, безусловно, ускоряет процесс деления, Согласно статистическим данным, в среднем число сложений и вычитании при использовании этого алгоритма сокращается в 2,67 раза.

Деление в избыточных системах счисления

Наиболее распространенные методы ускорения операции деления основаны на применении алгоритмов, где частное представляется в системе счисления, отличной от двоичной. Это означает, что цифры частного могут иметь больше, чем два значения, например <-1, 0, 1>, как это было в алгоритме умножения Бута, пли <-2 -1,0,1,2>. В таких системах одно и то же число может быть записано несколькими способами, из-за чего системы называют избыточными. Очередная цифра частного в избыточной системе счисления, в зависимости от базы этой системы, соответствует двум или более цифрам в двоичном представлении частного, и для нужного количества двоичных цифр частного остатка требуется меньше итераций. В то же время реализация такого подхода ведет к усложнению аппаратуры делителя, в частности надстраивается логика определения операции, выполняемой в очередной итерации. Для этой цели в состав устройства деления включается специальная память, хранящая таблицу, определяющую необходимые действия, и зависимости от текущей комбинации цифр в частичном остатке и делителе. Тем не менее выигрыш в быстродействии оказывается решающим моментом. Так, в микропроцессорах Pentium при делении мантисс чисел с плавающей занятой используется алгоритм SRT с базой 4, то есть частное сначала вычисляется с использованием цифр -2, -1, 0, 1, 2 с последующим преобразованном результата к стандартному двоичному представлению. В этом варианте выбор очередной цифры частного производится с помощью таблицы, состоящей из отдельных секций. Конкретную секцию определяют четыре старшие цифры делителя (после его нормализации). Входом в секцию служат шесть старших цифр частичного остатка. 40 в каждой итерации сдвигается не на один, а на два разряда, то есть число итераций сокращается вдвое. Известны варианты делителей, где берется еще большее основание системы счисления, в частности 8 и 16. В этом случае логика работы устройства существенно усложняется.

Операционные устройства с плавающей запятой

Операции над числами в формате с плавающей запятой (ПЗ) имеют существенные отличия от аналогичных операций целочисленной арифметики, поэтому их обычно реализуют с помощью самостоятельного операционного устройства. Как и целочисленное ОПУ, операционное устройство для чисел в формате ПЗ как минимум должно обеспечивать выполнение четырех арифметических действий; сложения, вычитания, умножения и деления.

После принятия стандарта IEEE 754 негласным требованием ко всем ВМ является обеспечение операций с числами, представленными в форматах, которые определены данным стандартом. Это требование не исключает использования в конкретной ВМ также иных форматов чисел с ПЗ, что обычно связано с сохранением совместимости с предыдущими моделями данной вычислительной машины.

Напомним основные положения записи чисел в стандарте IEEE 754. Мантиссы чисел М представляются в нормализованном виде, при этом действует прием скрытого разряда, когда старшая цифра мантиссы, всегда равная единице, в записи числа отсутствует, то есть в поле мантиссы старшей является вторая старшая цифра нормализованной мантиссы.

В отличие от общепринятого условия нормализации S = [М| |М| 2.

Запись числа содержит смещенный порядок, то есть порядок, увеличенный на величину смещения, которое в стандарте IEEE 754 для одинарного формата равно 127, а для двойного — 1023.

С учетом перечисленных особенностей арифметическую операцию над числами в формате с плавающей запятой можно записать в виде:

где Х М , Y M , Z M — нормализованные мантиссы операндов и результата; смещенные порядки операндов и результата; — знак арифметической операции. При всех различиях в выполнении разных арифметических операций подготовительный и заключительный этапы во всех случаях совпадают, в силу чего их имеет смысл рассмотреть отдельно

Первой особенностью операционных устройств для чисел с плавающей запятой является то, что в них операции над тремя составляющими чисел с ПЗ (знаками, мантиссами и порядками операндов) выполняются раздельно: блоком обработки знаков (БОЗ), блоком обработки порядков (БОП) и блоком обработки мантисс (БОМ). Для хранения операндов и результата в ОПУ предусмотрены соответствующие регистры. Хотя эти регистры могут быть физически реализованы в виде единых устройств, каждый из них логично рассматривать как совокупность трех регистров: знака, порядка и мантиссы. Таким образом, на этапе загрузки операндов в регистры ОПУ осуществляется «распаковка» чисел с ПЗ, их разбиение на три составляющие. В ходе такой распаковки в старшем разряде регистра мантиссы восстанавливается единица, которая в записи числа отсутствовала (была скрыта).

На предварительном этапе может быть также выполнена проверка на равенство нулю одного или обоих операндов (в стандарте IEEE 754 для представления нулевого значения используется такая запись числа, в которой нулю равны все Разряды порядка). Это позволяет исключить ненужные операции. Так, в операциях умножения и деления, если нулю равны множитель, множимое или делимое, в качестве результата сразу же можно принять нулевое значение, обойдя предвидимые данными операциями действия.

Действия на завершающем этапе выполнения любой арифметической операции, идентичны и сводятся к выявлению нулевого значения .мантиссы (потери значимости мантиссы), нормализации мантиссы, выявлению отрицательного переполнения порядка, «упаковке» составляющих результата.

Нулевое значение мантиссы может получиться в результате операции, например при сложении или вычитании мантисс. Второй причиной может стать сдвиг мантиссы вправо для устранения переполнения. В обоях случаях имеет место ситуация потери значимости мантиссы, и результат операции принимается равным нулю. Для стандарта IEEE 754 это означает, что все цифры порядка результата необходимо обнулить, а также то, что нормализацию мантиссы результата производить не нужно.

Нормализация мантиссы результата сводится к последовательному се сдвигу влево до тех пор, пока старшую позицию не займет единица. Каждый сдвиг сопровождается уменьшением на единицу порядка результата. В ходе уменьшения порядок может стать отрицательным, что для смещенных порядков свидетельствует о получение числа, непредставимого в данном формате. В такой ситуации результат принимается равным нулю и одновременно формируется признак потери значимости порядка.

В завершение мантисса результата округляется и, если это предусмотрено форматом ПЗ, из нее удаляется скрытый разряд.

В последней фазе осуществляется «упаковка» всех составляющих результата (знака, порядка и мантиссы), после чего сформированный результат заносится в выходной регистр ОГТУ.

Сложение и вычитание

В арифметике с плавающей запятой сложение и вычитание — более сложные операции, чем умножение и деление. Обусловлено это необходимостью выравнивания порядков операндов. Алгоритм сложения и вычитания включает в себя следующие основные фазы:

1. Подготовительный этап.

2. Определение операнда, имеющего меньший порядок, и сдвиг его мантиссы вправо на число разрядов, равное разности порядков операндов.

3. Приравнивание порядка результата большему из порядков операндов.

4. Сложение или вычитание мантисс и определение знака результата.

5. Проверку па переполнение.

6. Заключительный этан.

Операции предшествует вышеописанный подготовительный этап, в ходе которого операнды «распаковываются» и помещаются в регистры ОПУ.

Сложение и вычитание выполняются идентично, но в случае вычитания необходимо изменить знак второго операнда на противоположный. Далее производится проверка с целью выяснения, не равен ли нулю один из операндов. Если это имеет место, в качестве результата сразу берется другой операнд.

В следующей фазе осуществляется такое преобразование одного из исходных чисел, чтобы порядки обоих операндов стали равны. Для пояснения рассмотрим например сложения десятичных чисел с ПЗ:

123 х 100 +456 х 10 -2 .

Очевидно, что непосредственное сложение мантисс недопустимо, поскольку цифры мантисс, имеющие одинаковый вес, должны располагаться в эквивалентных позициях. Так, цифра 4 во втором числе должна суммироваться с цифрой 3 в первом. Этого можно добиться, если записать второе число так, чтобы порядки обоих чисел были равны:

123 х 10 0 + 456 х 10-2 = 123 х 10° + 4,56 х 10° = 127,56 х 10°.

Выравнивания порядков можно достичь сдвигом мантиссы меньшего из чисел вправо, с одновременным увеличением порядка этого числа, либо сдвигом мантиссы большего из чисел влево и уменьшением его порядка. Оба варианта сопряжены с потерей цифр мантиссы, но выгоднее сдвигать меньшее из чисел, так как при этом теряются младшие разряды мантиссы. Таким образом, выравнивание порядков операндов реализуется путем сдвига мантиссы меньшего из чисел на один разряд вправо с одновременным увеличением порядка этого числа на единицу. Действия повторяются до совпадения порядков. Если в процессе сдвига мантисса обращается в 0, в качестве результата операции берется другой операнд.

Следующая фаза — сложение мантисс с учетом их знаков, что при одинаковых знаках мантисс может привести к переполнению. В последнем случае мантисса результата сдвигается вправо на один разряд, а порядок результата увеличивается на единицу. Это, в свою очередь, чревато переполнением поля порядка. Тогда операция прекращается и формируется признак переполнения, сопровождаемый соответствующим предупреждением (обычно в виде сигнала прерывания).

Далее выполняется описанный выше заключительный этап.

В отличие от целочисленной арифметики, в операциях с ПЗ сложение и вычитание производятся приближенно, так как при выравнивании порядков происходит потеря младших разрядов одного из слагаемых. В этом случае погрешность всегда отрицательна и может доходить до единицы младшего разряда.

На начальном этапе умножения чисел с ПЗ производится проверка на равенство нулю одного из сомножителей. Если один из операндов равен нулю, в качестве Результата выдается 0, представленный в данном формате чисел с ПЗ. Следующий шаг — сложение порядков. Если в рассматриваемом формате используется смещенный порядок, то в полученной сумме будет содержаться удвоенное смещение, поэтому из нее необходимо вычесть величину смещения. Результатом действий с порядками может стать как переполнение порядка, так и потеря значимости. В обоих случаях выполнение операции прекращается и выдается соответствующее сообщение (возникает прерывание).

Если порядок результата лежит в допустимых границах, на следующем шаге производится перемножение мантисс с учетом их знака, которое выполняется так же как для чисел с фиксированной запятой. При размещении произведения мантисс в разрядной сетке необходимо учитывать, что мантиссы представлены не целыми числами, а правильными дробями. Хотя результат умножения мантисс имеет удвоенную по сравнению с операндами длину, он округляется до длины поля мантиссы.

На последнем шаге производится нормализация и компоновка результата аналогично тому, как это имеет место при сложении и вычитании. Отметим, что при нормализации результата возможно переполнение порядка.

Сначала также проводится проверка на 0. Если нулю ранен делитель, в зависимости от реализации выдается сообщение о делении на 0, либо в качестве результат принимается бесконечность (для этого в некоторых форматах ПЗ имеется специальная кодовая комбинация). Когда нулю равно делимое, результат также принимается равным нулю.

Далее выполняется вычитание порядка делителя из порядка делимого, что приводит к удалению смещения из порядка результата. Следовательно, для получения смещенного порядка результата к разности должно быть добавлено смещение. После выполнения этих действий необходима проверка на переполнение порядков и потерю значимости.

Следующий шаг — деление мантисс, за которым идут нормализация, округление и компоновка числа из мантиссы и порядка.

Реализация логических операций

Помимо арифметических действий ОПУ любой вычислительной машины предполагает выполнение основных логических операций и сдвигов. Чаще всего такие операции реализуются дополнительными схемами, входящими в состав целочисленных ОПУ.

К базовым логическим операциям относятся: логическое отрицание (НЕ), логическое сложение (ИЛИ) и логическое умножение (И). Этот набор, как правило, дополняют операцией сложения по модулю 2 (исключающее ИЛИ).

Рис. 7.55. Структура операционного блока для выполнения логических операций

Булева переменная в ВМ представляется едким битом, однако на практике логи ческие операции в ОПУ выполняются сразу над совокупностью логических переменных, объединенных в рамках одного байта или машинного слова, причем над всеми битами этого слова выполняется одна и та же операция. Поскольку каждый бит совокупности логических переменных рассматривается как независимая переменная, никакие переносы между разрядами не формируются. Операционный блок (ОПБ) для выполнения логических операций обеспечивает реализацию всех перечисленных логических операций. Возможная структура подобного ОПБ по дамана рис 7.55.

Выбор нужной операции осуществляется с помощью двухразрядного управляющего кода L (l 1 l 0 ). С учетом управляющего кода выходная функция Z может быть описана выражением:

1. Охарактеризуйте состав операционных устройств, входящих в АЛУ. Из каких соображений и каким образом он может изменяться?

2. Поясните понятие «операционные устройства с жесткой структурой». В чем заключается жесткость их структуры? Каковы их достоинства и недостатки?

3. Чем обусловлено название операционных устройств с магистральной структурой? Сравните магистральные структуры е жесткими структурами, выделяя достоинства, недостатки и область применения.

4. Дайте развернутую характеристику классификации операционных устройств с магистральной структурой. Поясните достоинства и недостатки «минимального» и «максимального» вариантов.

5. Поясните функциональный состав параллельного операционного блока магистрального ОПУ. Каким образом можно минимизировать количество внешних связей этого блока? Ответ сопроводите конкретным примером.

6. Чем обусловлена специфика целочисленного сложения и вычитания? Какую роль играет в них дополнительный код? К чему бы привел отказ от дополнительного кода? Ответ поясните па примерах. Как выявляется переполнение в этих операциях?

7. Сформулируйте достоинства, недостатки и область применении четырех вариантов целочисленного «традиционного» умножения. Как учитываются знаки сомножителей?

8. Охарактеризуйте суть двух групп логических методов ускорения умножения.

9. Попарно сравните алгоритм Бута, модифицированный алгоритм Бута, алгоритм Лемана.

10. Разработайте алгоритм умножения с обработкой за шаг трех разрядов множителя.

11. Поясните суть аппаратных методов ускорения умножения, выделив три возможных подхода.

12. Сравните умножители Брауна, Бо-Вули, Пезариса. Чем они схожи и в чем отличаются друг от друга?

13. В чем заключается основная идея древовидных умножителей? Каковы особенности их организации?

14. Сформулируйте, в чем состоит сходство и различие дерева Уоллеса, дерева Дадда и перевернутого ступенчатого дерева.

15. С какой целью и каким образом выполняется конвейеризация матричных и древовидных умножителей? Приведите (и поясните) конкретные примеры

16. На конкретном примере объясните, как можно нарастить разрядность аппаратного умножителя.

17. Сравните организацию целочисленного деления с восстановлением остатка и без восстановления остатка. Как учитываются при делении знаки операндов?

18. Обоснуйте возможность совмещения структур умножителя и делителя. Опишите объединенную структуру.

19. Сформулируйте четыре пути ускорения целочисленного деления. Сравните между собой их возможную реализацию.

20. Какие из операций с плавающей запятой считаются наиболее сложными? Ответ обоснуйте на конкретных примерах.

21. В чем состоит специфика умножения с плавающей запятой? Поясните эту специфику на примере.

22. Разработайте серию примеров для иллюстрации всех особенностей деления с плавающей запятой.

23. Создайте структуру операционного блока для выполнения как сложения/вычитания, так и базового набора логических операций. Обоснуйте каждый элемент этой структуры.